EKV Model

Enz-Krummenaker-Vittoz (EKV) Model has been developed in EPFL. Today is a widely used (these men planified years ago to conquer the world!) for CMOS technologies and simulators.

In this page I will summarize the main equations of the model useful for analog IC design.

If you are more interested, take a look at the book!

Charge-Based MOS Transistor Modeling: The EKV Model for Low-Power and RF IC Design
Christian C. Enz, Eric A. Vittoz
Wiley
July 2006
ISBN: 978-0-470-85541-6

Pinch-off voltage:                    $ V_p\simeq \frac{V_g-V_t}{n}$

Saturation voltage:                  $ V_{d,sat}=V_p-V_s$

Technology parameter:            $ \beta=k_p\frac{W}{L}=\mu C_{ox}\frac{W}{L}$

Specific current:                      $ I_s=2n\beta U_t^2$

SATURATION $latex (V_D>V_p)$

Strong Inversion (SI)                 $latex I_{D,sat}=\dfrac{\beta}{2n}(V_g-V_{t}-nV_s)^2=\dfrac{\beta n}{2}(V_p-V_s)^2=\dfrac{\beta n}{2}V_{d,sat}^2$

Weak Inversion (WI)                 $latex I_{D,sat}=I_{s} e^{\frac{V_g-V_t}{nU_t}} \left(e^{\frac{-V_s}{U_t}}-e^{\frac{-V_d}{U_t}}\right)$

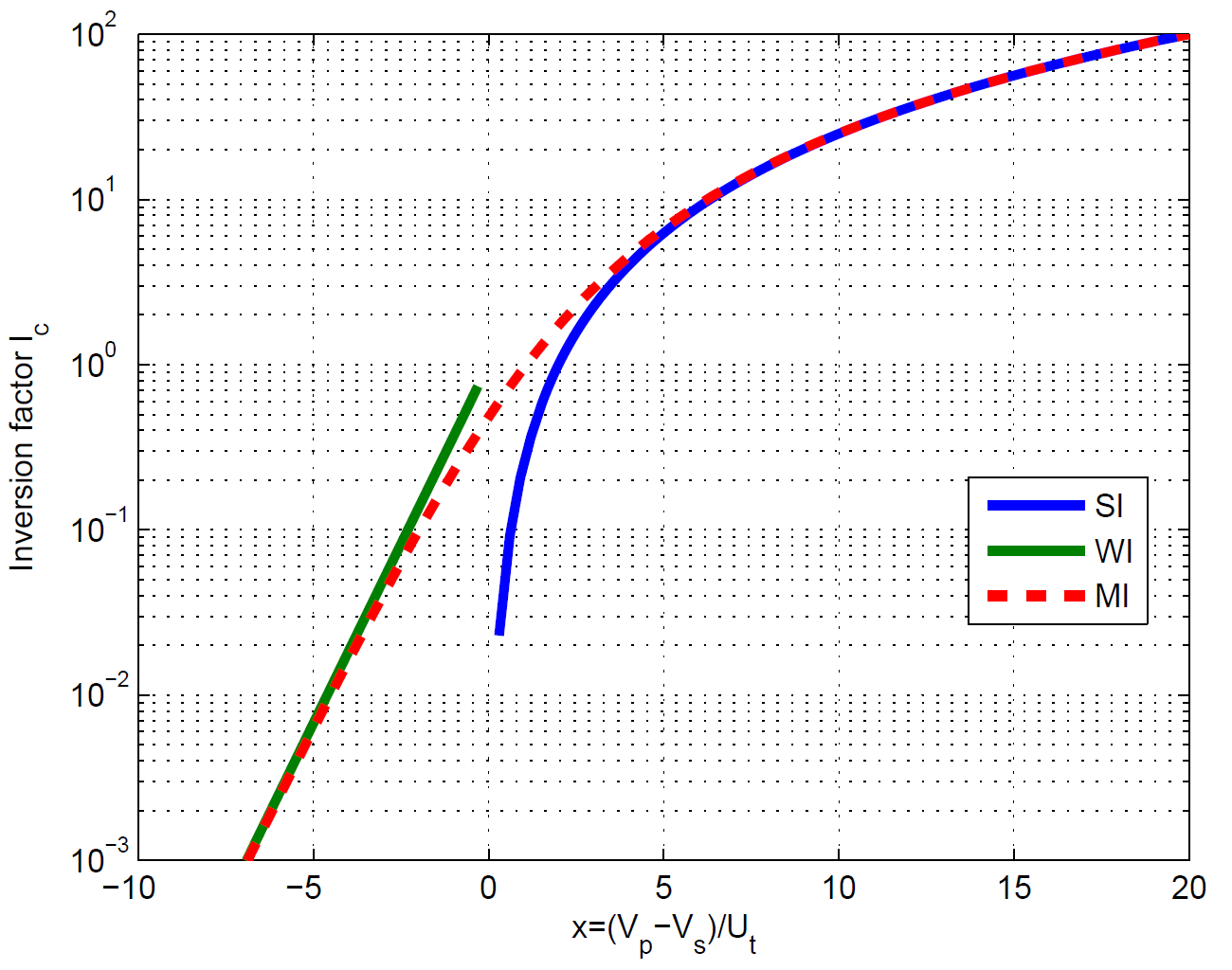
In terms of specific current we can write exponential (WI) and quadratic (SI) behavior of saturation current. In moderate inversion (MI), an approximation can be used:

SI $ \Rightarrow I_{d,sat}=I_s\left(\dfrac{V_p-V_s}{2U_t}\right)^2$     WI $latex\Rightarrow I_{d,sat}\simeq I_s e^{\frac{V_p-V_s}{U_t}}$     MI $latex\Rightarrow I_{d,sat}\simeq I_s ln^2\left(1+e^{\frac{V_p-V_s}{U_t}}\right)$

We define the inversion factor $latex I_c$ as: $latex I_c=\dfrac{I_{d,sat}}{I_s} \Rightarrow \left\{ \begin{matrix} SI && I_c>10 \\ MI && 0.1<I_c<10 \\ WI && I_c<0.1 \end{matrix}\right.$

Imposing a bias on the gate is equivalent to set the inversion factor (see graph below).

close all, clear all, clc

x=linspace(-10,20);

y1=(x/2).^2;

y2=exp(x);

y3=(log(1+exp(x/2))).^2;

semilogy(x(length(x)/3+1:end),y1(length(x)/3+1:end),x(1:length(x)/3),y2(1:length(x)/3),x,y3,'r--','linewidth',3)

hold on, grid on

ylim([1e-3,1e2])

legend('SI','WI','MI','Location','Best')

xlabel('x=(V_p-V_s)/U_t')

ylabel('Inversion factor I_c')