- français
- English
Metric determination
Requirements for the distance between two corpuses d(C1, C2):
- Normalization: 0 <= d(C1,C2) <= 1
- Distance between a corpus and itself is zero: (C1 = C2 ) → d(C1,C2 ) = 0
- Symmetry: d(C1,C2) = d(C2,C1)
- The distance should be similar for consecutive years while increasing as years are distant
- Is independant of the size of the corpus
Matrix representation:
year1 year2 year3 ... yearN
year1 0 d(1,2) d(1,3) ... d(1,N)
year2 d(2,1) 0 d(2,3) ... d(2,N)
year3 d(3,1) d(3,2) 0 ... d(3,N)
... ... ... ... ...
yearN d(N,1) d(N,2) d(N,3) ... 0
Criteria to juge if a metric is better than another one:
- Classification: Separate the articles in a training and a testing set. Determine the year of each article in the testing set by computing the distance of the given article with every year from the training set. Prediction error quantifies the "goodness" of the metric
-
Upon clustering according to the metric, consecutive years should be assigned to the same cluster.
-
Robustness:
-
The size of the corpus shouldn't influence the distance. Thus, the distance between a subset of C1 from C2 should be the same that the distance between the whole corpus C1 and C2.
-
The distance should be robust considering OCR unresolved errors.
-
-
Datation efficiency: when computing the distance of an article from the each year or years intervals, the smaller distance should assign the text to a year with 5 years margin.
-
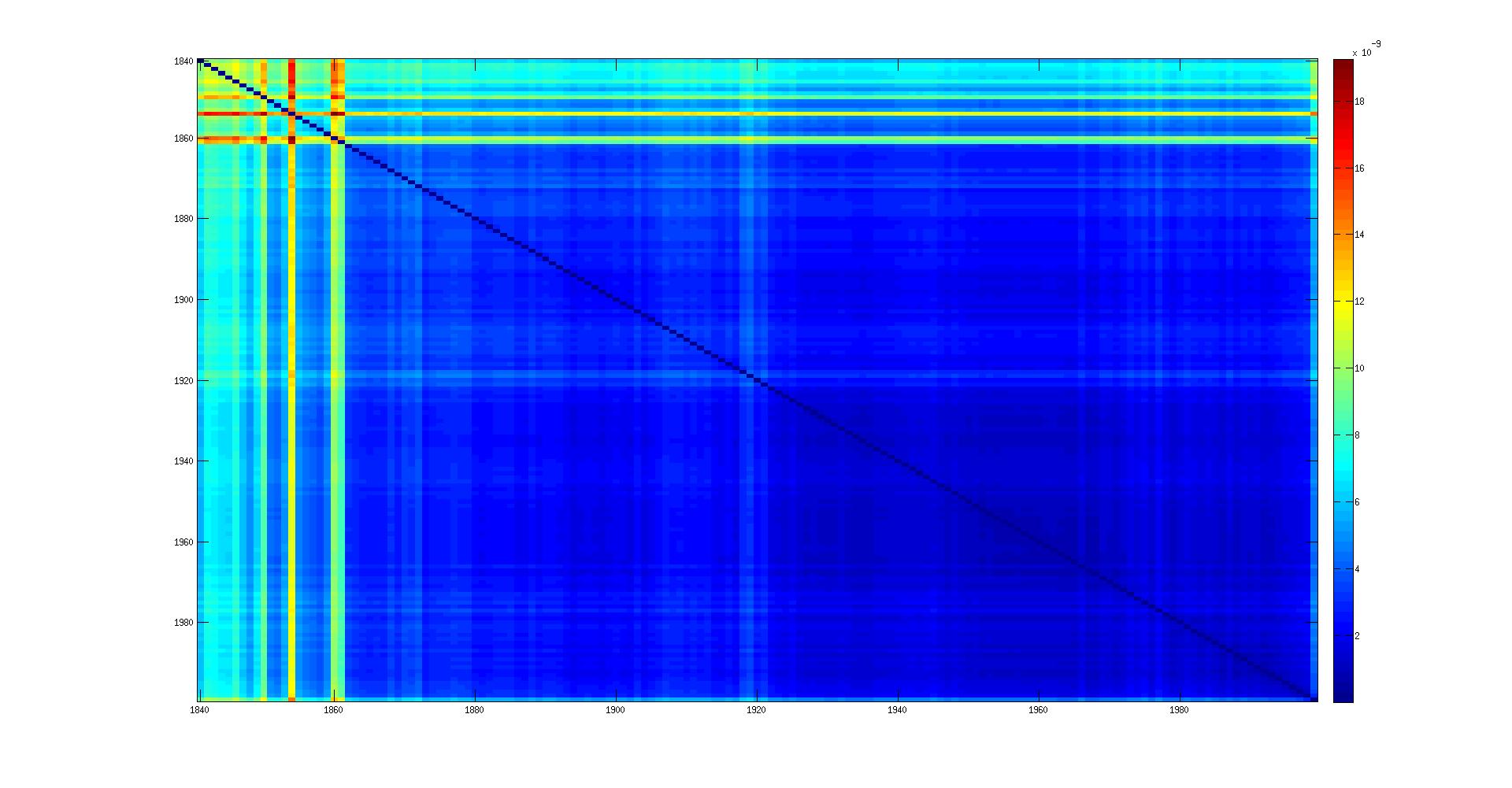
In the matrix plot: the color should fade out homogeneously from the diagonal to the opposite corners. There should be a kind of 'band' around the diagonal.
Choices of distances:
- First simple metric:
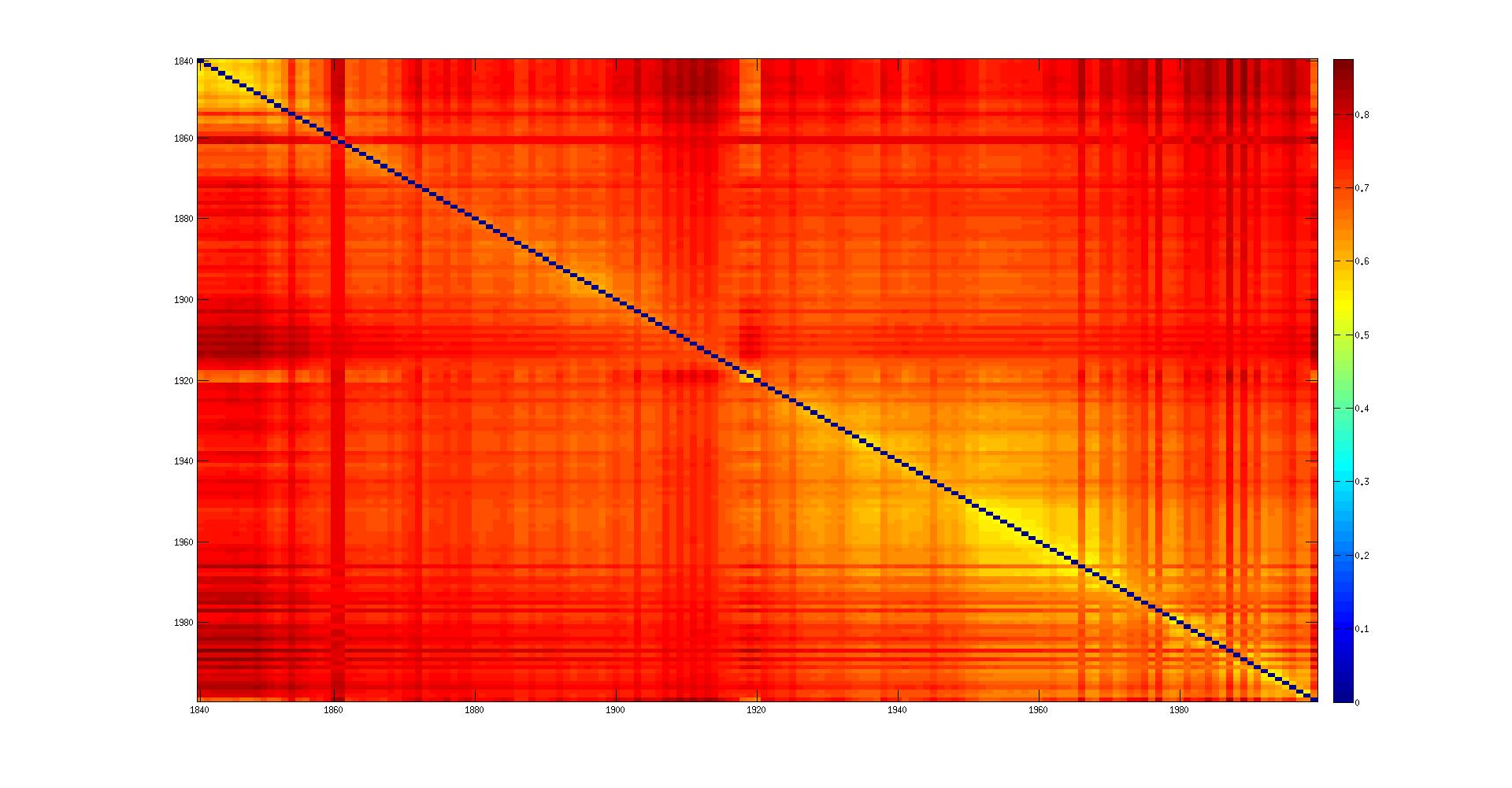
d(C1,C2) = 1 - 2 || C1 ∩ C2 || / ( || C1 || + || C2 || )
Intuitive metric based on the word that appear and disappear from the language.
Here is the distance matrix on corrected ocr:
- Kullback-Leibler Divergence:
- The Kullback-Leibler Divergence between P and Q is a measure of the information lost when Q is used to approximate P.
- Formula from Wikipedia :

- Adding a Dirichlet smoothing to avoid value 0.0 which is a problem for the division
- (see this link for more informations : http://www.mansci.uwaterloo.ca/~msmucker/publications/Smucker-Smoothing-IR319.pdf)
RESULTS (Left is with Correction of OCR, right is without it) :
1-grams
- Divergence matrix with the probability of each word per year :
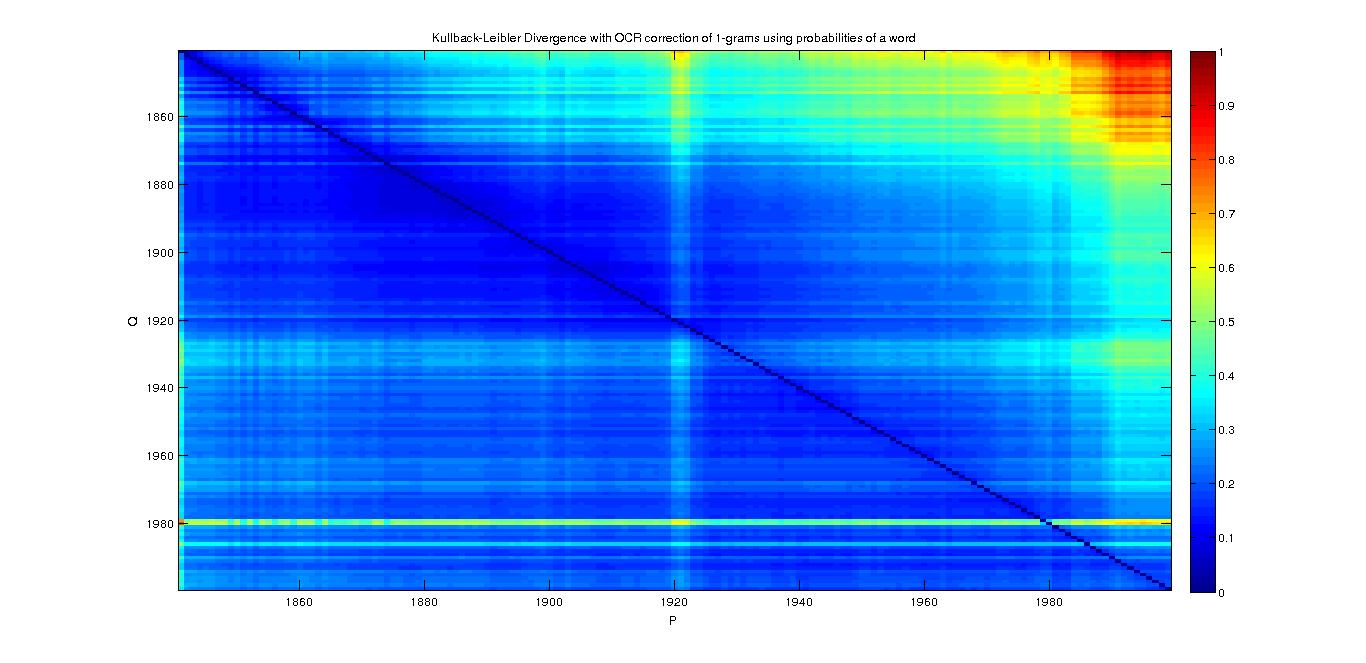
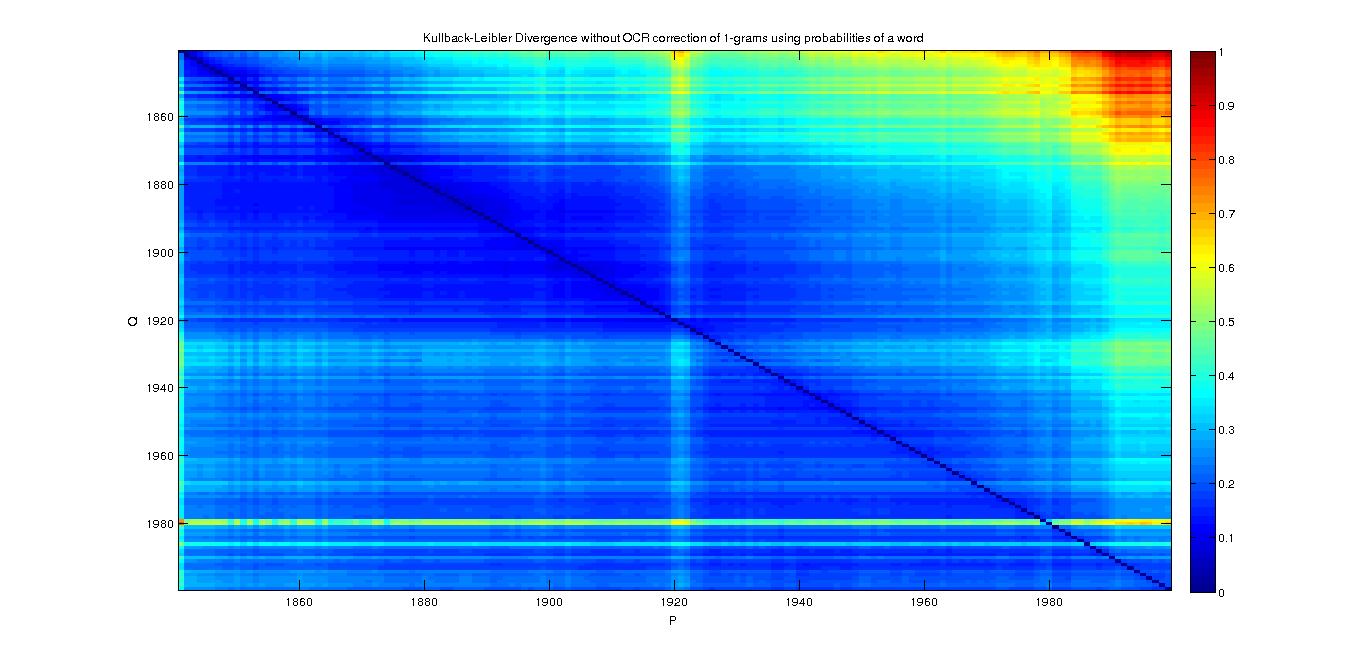
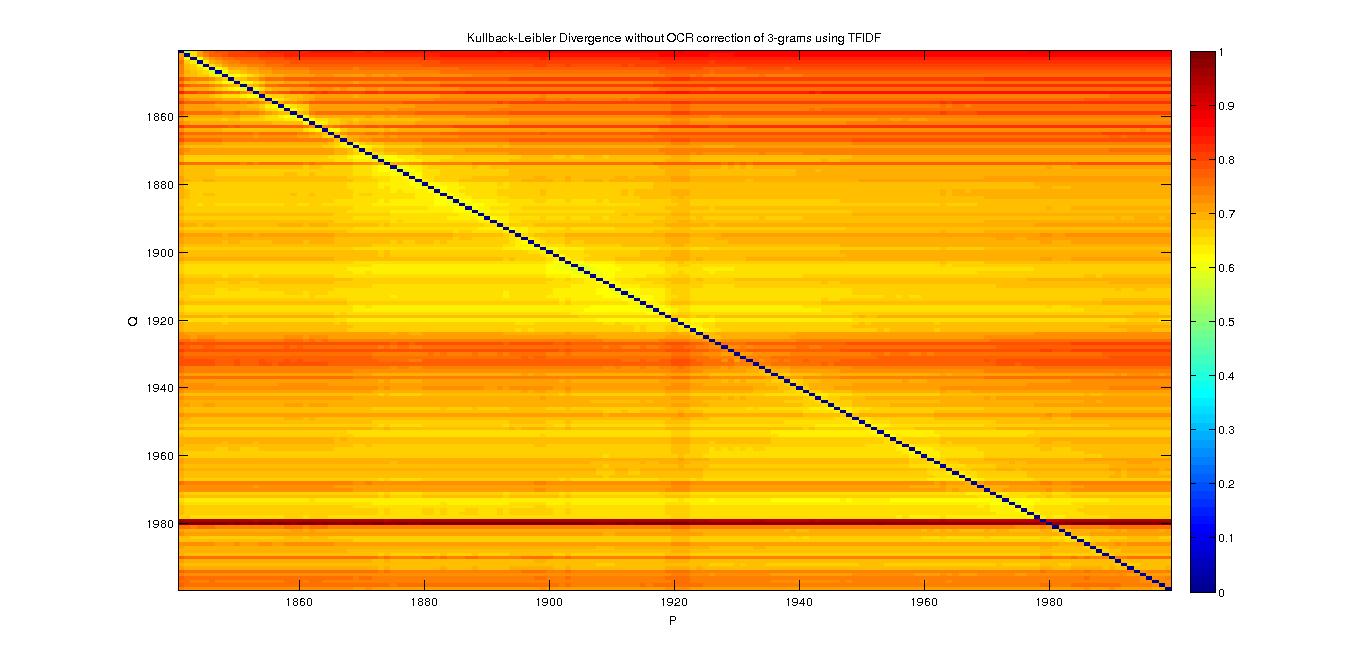
- We can see that when we approximate the 1990's years with the 1840's, we have a big divergence, but it is not the case in the other direction.
- For the year 1980, we don't know how to explain that it is a bit more divergent.
- Divergence Matrix with TF-IDF values :
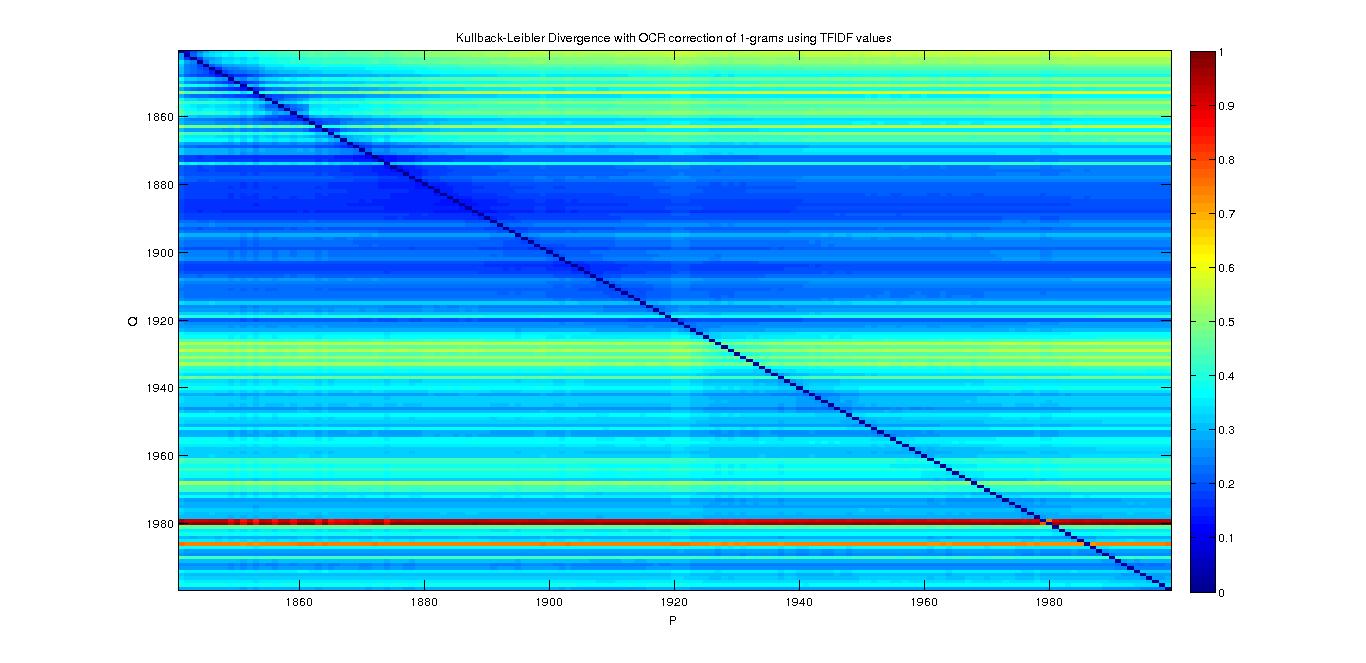
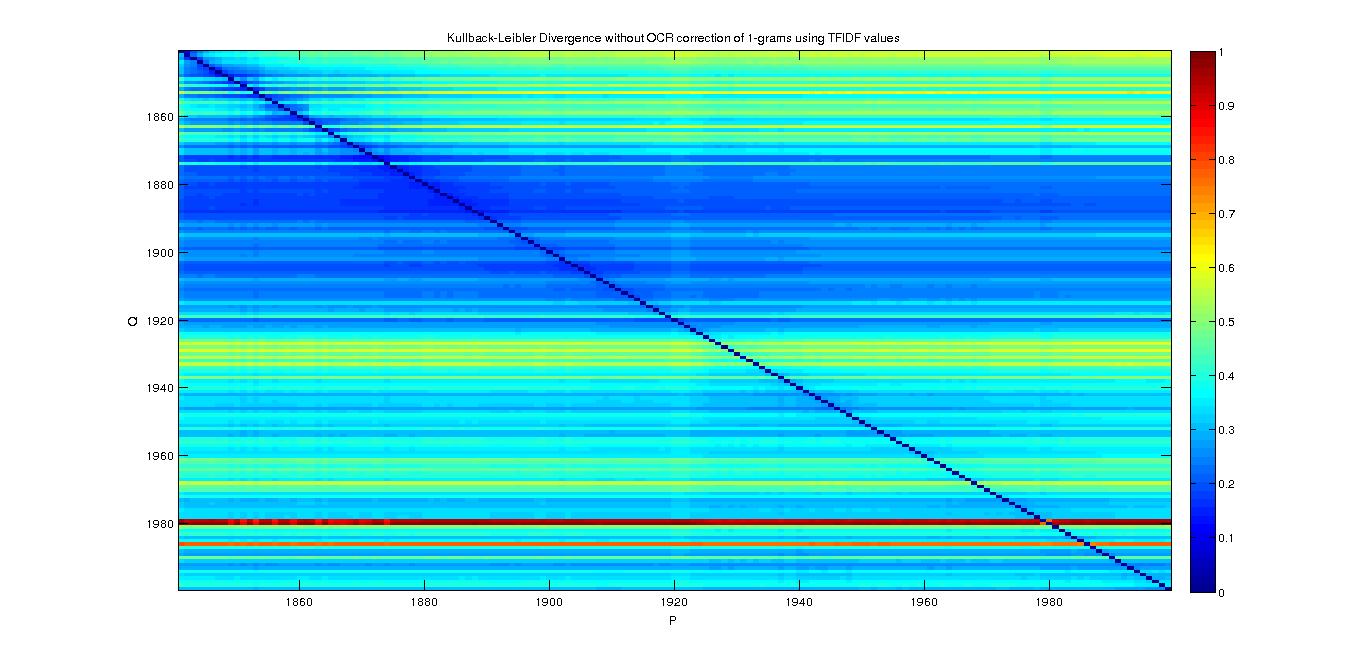
- We can observe a strange result. Is it because of the TF-IDF ? Of course ! If we do not consider (or with a really small weight) the common words to all years, the divergence between years is big...
- ... But it doesn't explain completly why we have some linear divergence for on specific year compare to all the others...
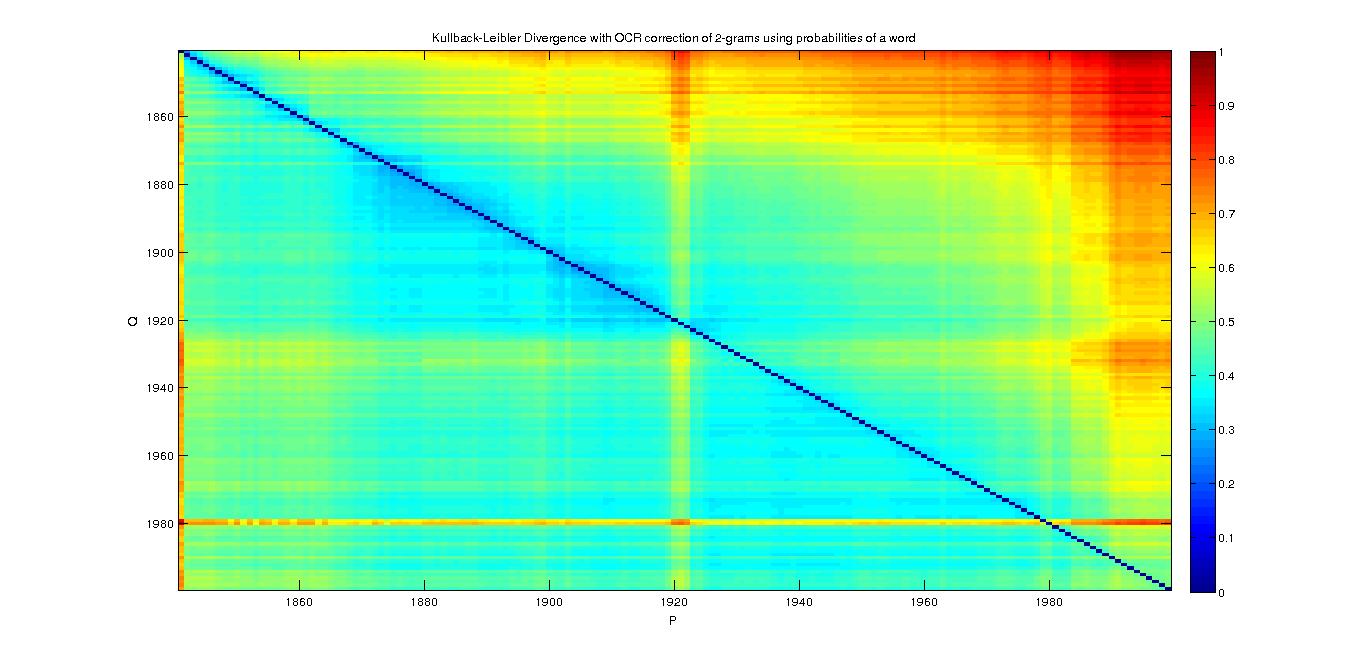
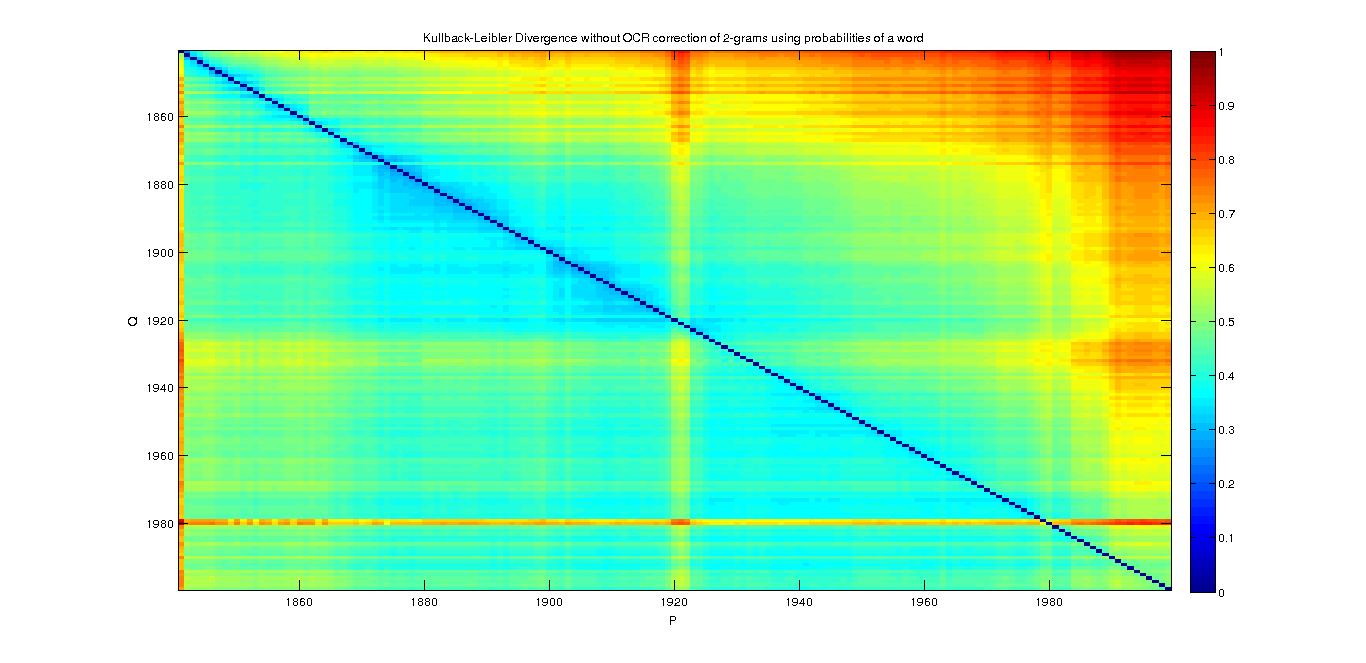
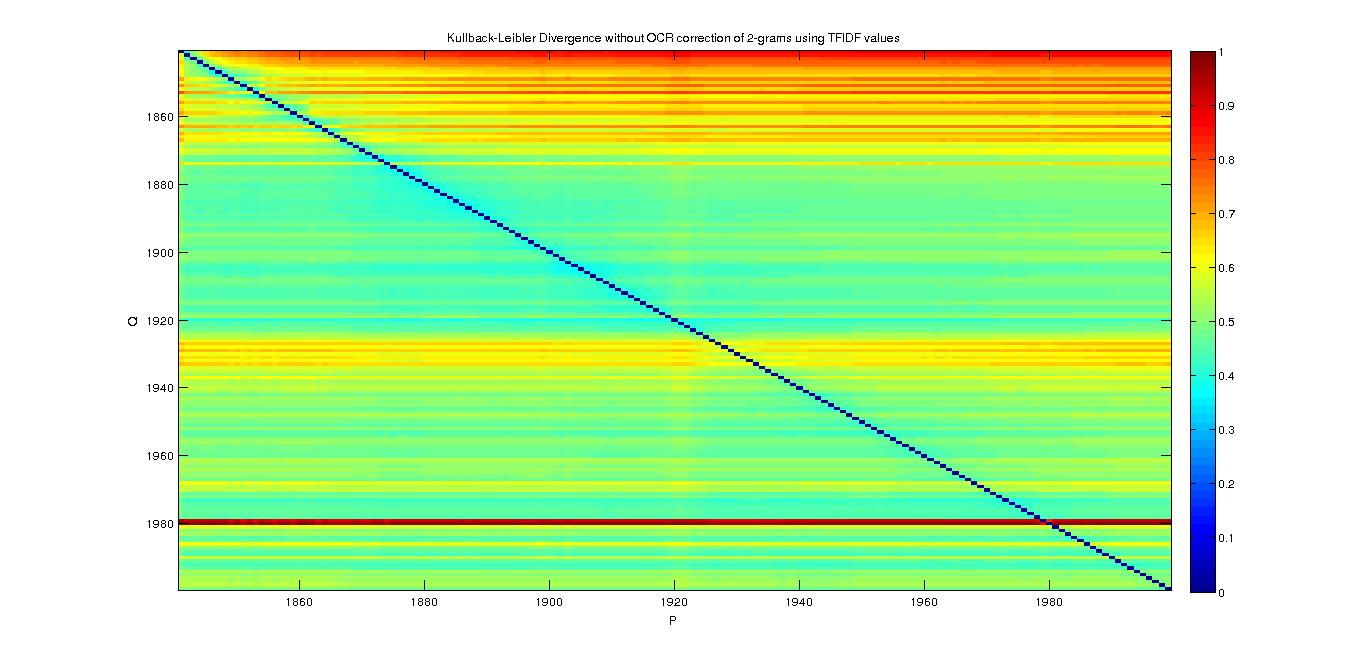
2-grams
- With Probability of a word
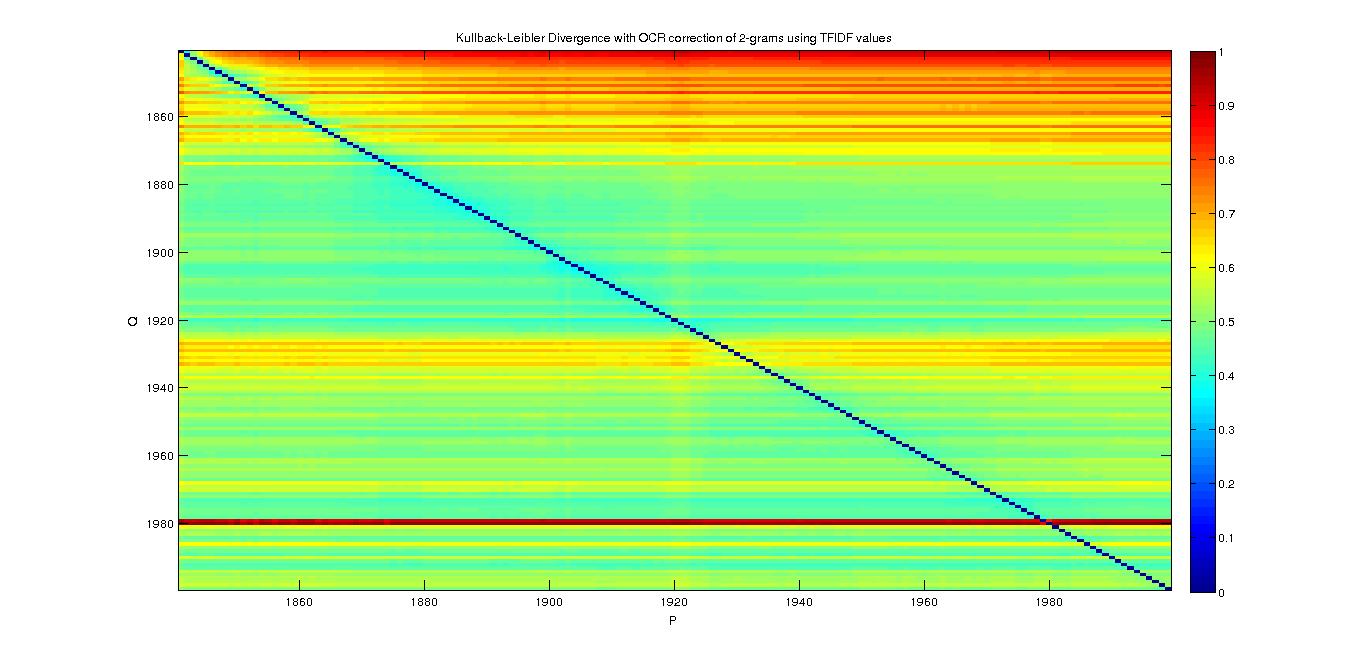
- With TFIDF
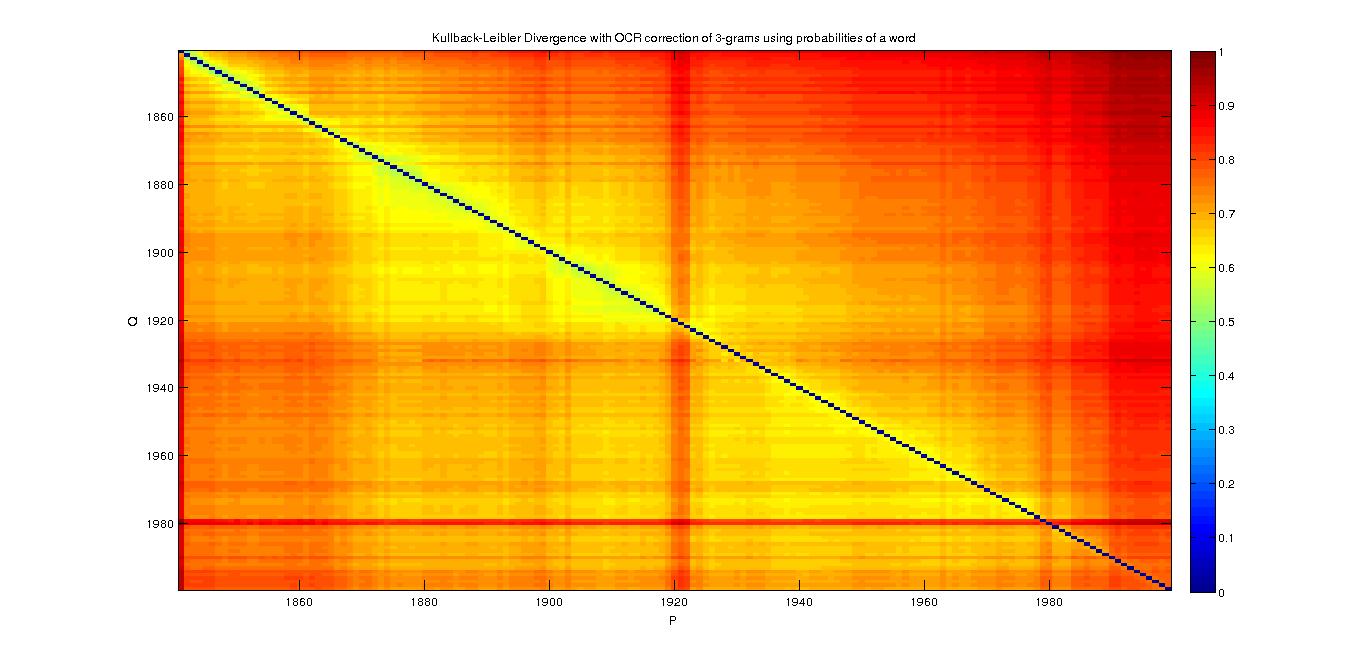
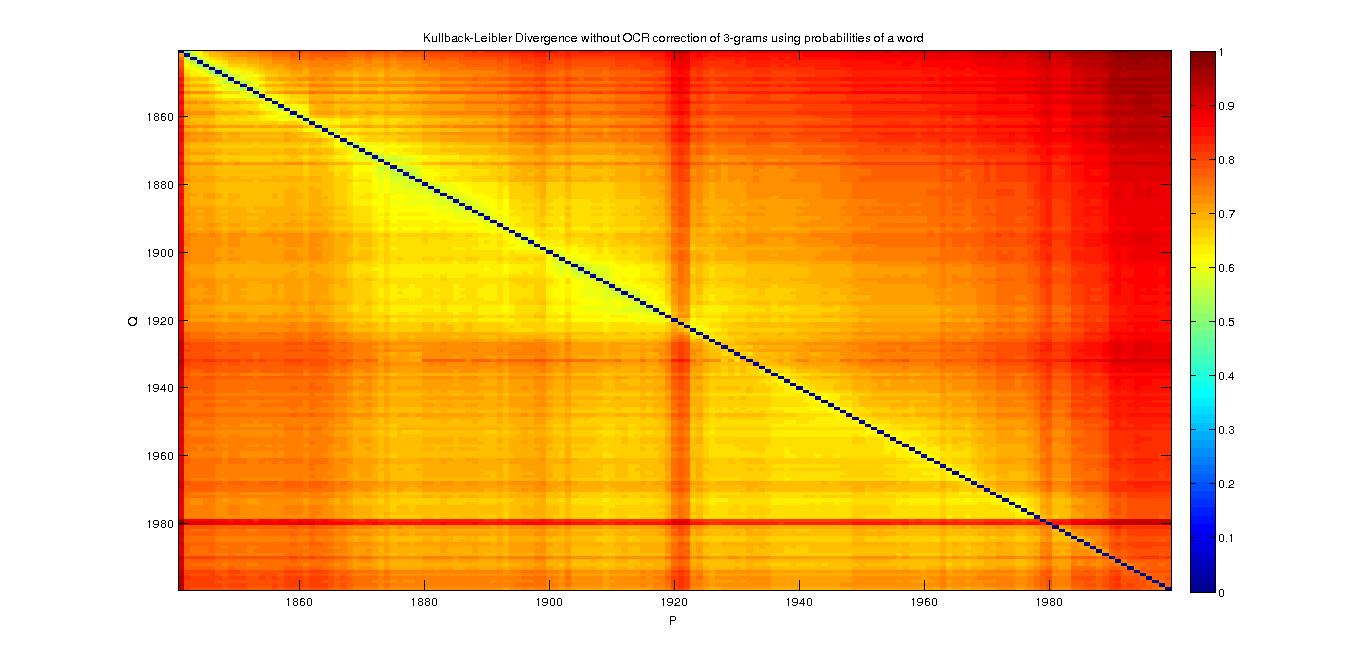
3-grams
- With the probability of a word
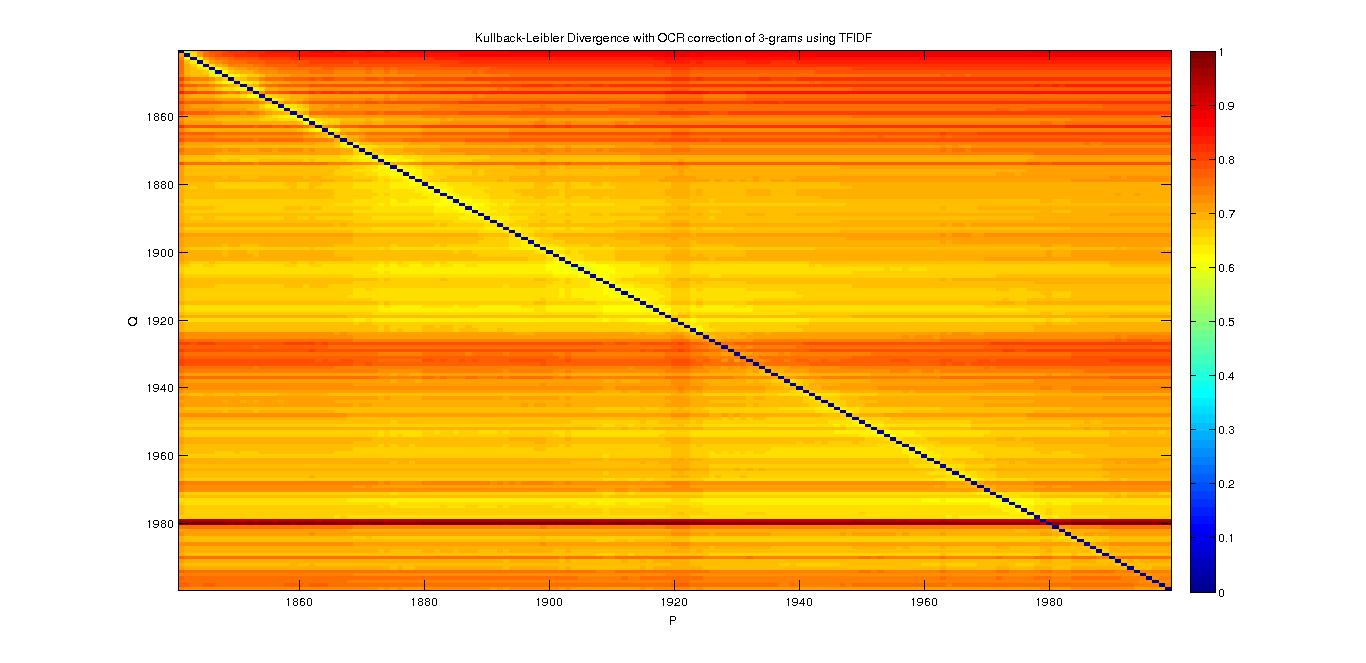
- With TFIDF
- Cosine: the distance is 1 - cosine_similarity
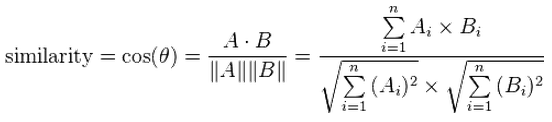
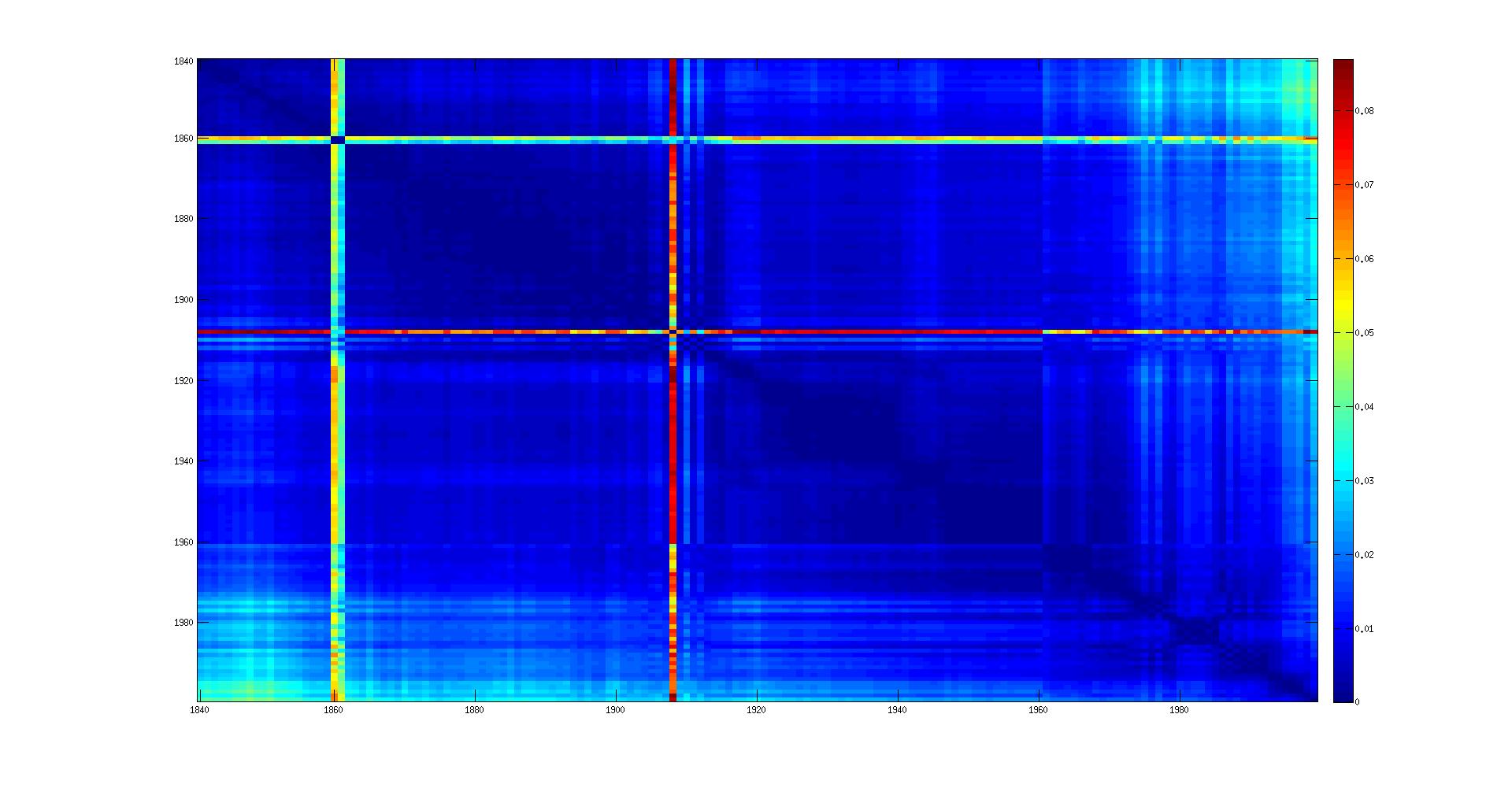
where Ai is the frequency of word i in year A and the same for Bi- Distance on the ocr without corrections:
- Distance on the corrected ocr:
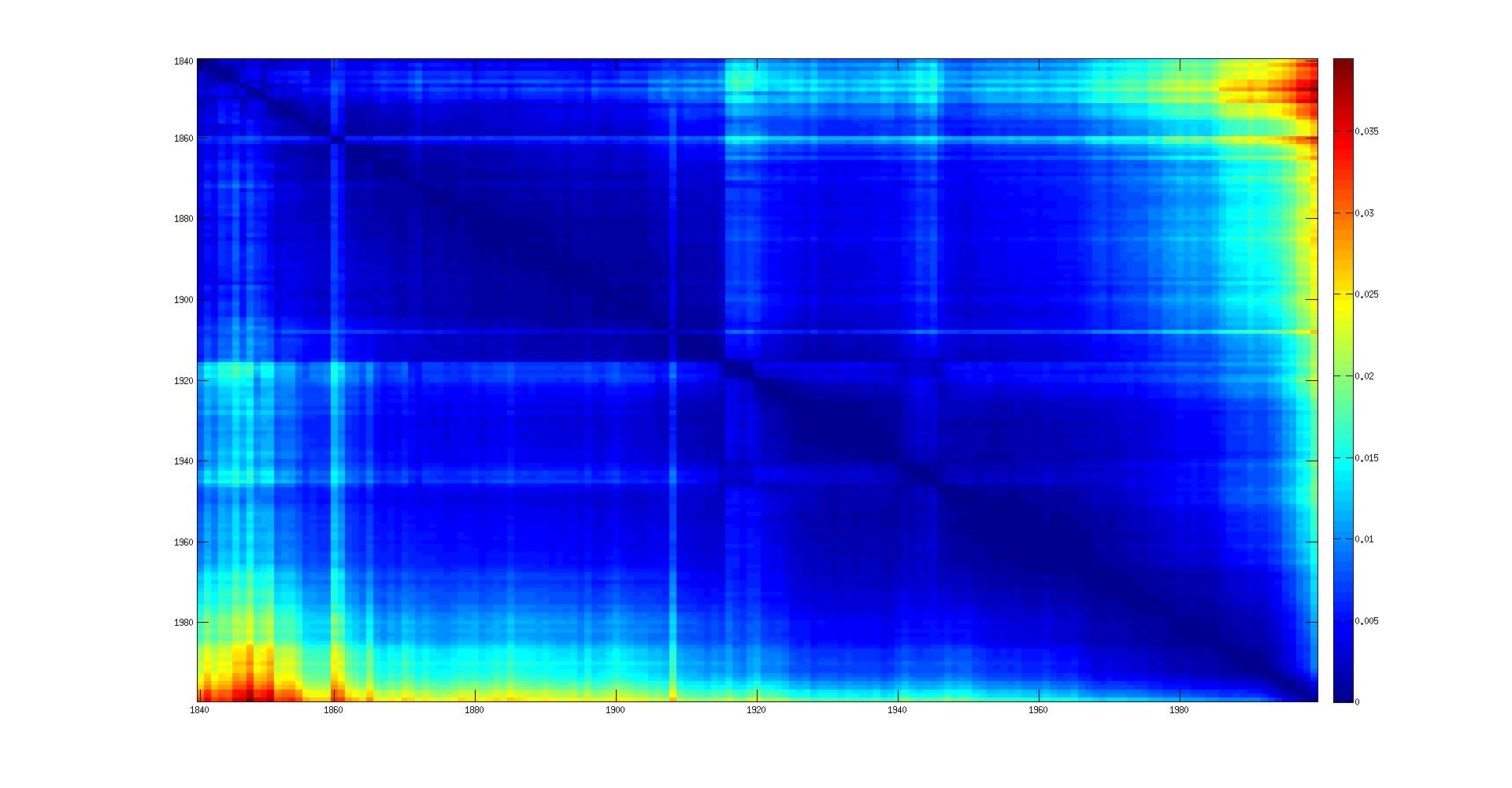
- Corrected with tf-idf:
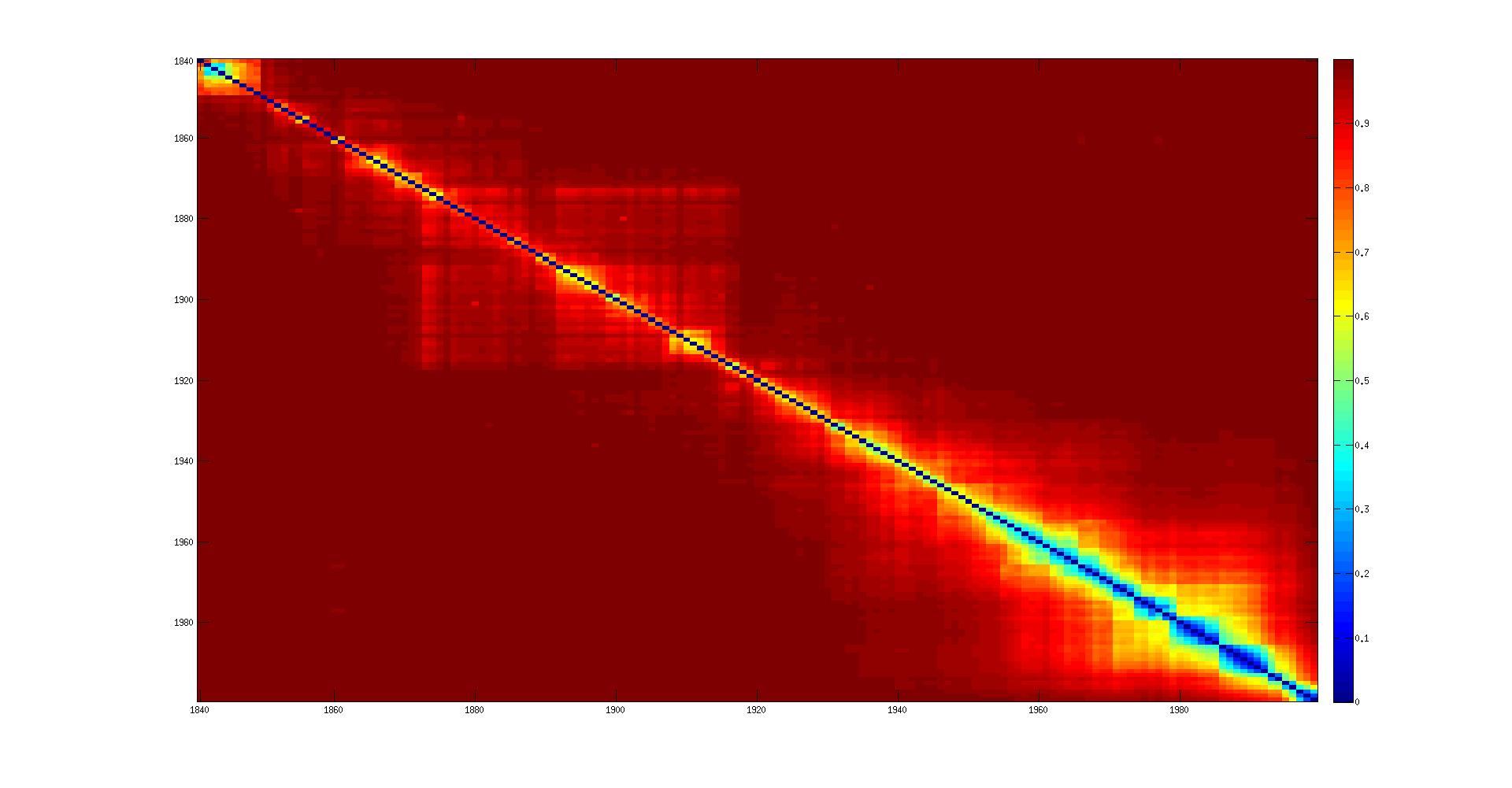
- Distance on the ocr without corrections:
Chi-square
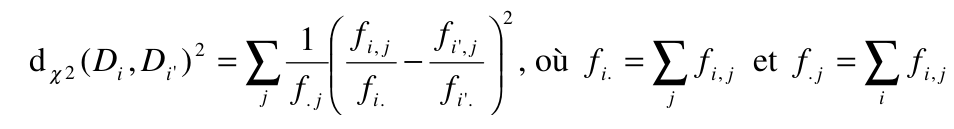
where fi,j is the frequency of the word j in the year i.
- on the corrected ocr:
- Out-of-place measure (Cavnar and Trenkle, 1994) This metric allows us to consider the change in the importance of common word of the two corpuses. The rank of the n-gram is its order by its frequency. If a word appears or disappear it has a maximum value rank. Otherwise, we sum to the metric the change of rank of the n-gram.
In the experiment, the Out-of-place measure is divided to two methods (i.e., whether to use the unmatched word's frequency. Besides, since the author of this metric mentioned in his paper that this method provides high robustness in the face of OCR error, thus the effect of OCR correction is not clear in this method (It has few changes in ratio but more in count). Results are as follows:
- Only use matched word's difference.
For corrected dataset
For uncorrected dataset
- Use whole word, and those unmatched words have a maximum value rank.
For corrected dataset
For the uncorrected dataset
- Ce wiki
- Cette page
