Contents

% bpdq_demo_2d : Demo for BPDQ-TV reconstruction in 2-d
%
% This demo creates a synthetic angiogram image, takes randomly subsampled
% Fourier measurements, and quantizes the measurements.
%
% Then the BPDQ-TV algorithm is run to reconstruct the image from the
% quantized measurements.
%
% This file is part of BPDQ Toolbox (Basis Pursuit DeQuantizer)
% Copyright (C) 2009, the BPDQ Team (see the file AUTHORS distributed with
% this library) (See the notice at the end of the file.)

% With parameters as set in this demo, execution time was 120 seconds
% on 2.4 GHz Intel Core 2 Duo processor.

Demo Parameters

Note: (Quantization threshold alpha is computed depending on nbins and on the signal instance)

N=256;
fsubfactor=6;
p=10;
alpha=50;
nellipse=10;
aseed=6;
seed=1;

bpdq_opts={'dr_gamma',.1,'dr_lambda',1,'dr_verbosity',0,'dr_maxiter',50};

dim=[N,N];
fprintf('Generating %g x %g synthetic angiogram\n',N,N);
im=bpdq_generate_angiogram(N,N,nellipse,aseed);

K=.5*floor(N^2/fsubfactor);
fprintf(['Selecting %g random fourier locations, i.e. 1/%i of the %g ' ...
         'available\n'],2*K, fsubfactor, N^2);
rand('seed',seed);
[useind,loc]=bpdq_random_fourier_locations(dim,K,'forcecenter',1);

Generating 256 x 256 synthetic angiogram
Selecting 10922 random fourier locations, i.e. 1/6 of the 65536 available

Defining Fourier subsampling operators

samp=@(x) bpdq_fft_subsample(x,useind,dim);
samp_t=@(x) bpdq_fft_subsample_t(x,useind,dim); % transpose of samp

Some utility functions

unpack complex vector into vector of reals

c2r = @(x) [real(x(:));imag(x(:))];
r2c = @(x) x(1:end/2)+sqrt(-1)*x(end/2+1:end);

% "complete" measurement operators (from sparsity domain to measurements)
A=@(x) samp((x(:)));
At=@(x) vec(samp_t(x));

Making measurements

fprintf('Computing quantized measurements alpha=%g\n',alpha);

y=samp(im);

% quantize
yq=bpdq_quantize(y,alpha);
Nbins=2*max(abs(c2r(y)))/alpha; % equivalent # of bins

% fprintf('%g equivalent number of quantization bins\n',Nbins);

% Compute epsilon for BPDQ program
dM=numel(useind);
M=2*dM;

Computing quantized measurements alpha=50

Running BPDQ-TV

fprintf('Running BPDQ-TV reconstruction with p=%g\n',p);
epsilon = bpdq_err_p(p,alpha,M);
[xstar,D_bpdq]=bpdq_2d_tv(yq,A,At,dim,epsilon,p,bpdq_opts{:});
im_bpdq=real(reshape(xstar,dim));
SNR_bpdq= bpdq_compute_snr(im,im_bpdq);

Running BPDQ-TV reconstruction with p=10

Running BPDN-TV (p=2)

fprintf('Running BPDN-TV (p=2) reconstruction\n');
epsilon2 = bpdq_err_p(2,alpha,M);
[xstar2,D_bpdn]=bpdq_2d_tv(yq,A,At,dim,epsilon2,2,bpdq_opts{:});
im_bpdn=real(reshape(xstar2,dim));
SNR_bpdn=bpdq_compute_snr(im,im_bpdn);

rmin=min([im(:);im_bpdn(:);im_bpdq(:)]);
rmax=max([im(:);im_bpdn(:);im_bpdq(:)]);
drange=[rmin,rmax];

Running BPDN-TV (p=2) reconstruction

Displaying results

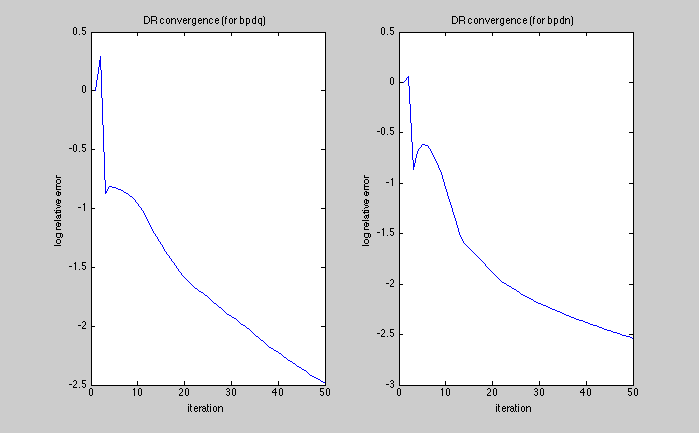
fprintf('Displaying results and convergence curves\n');
figure(1)
fprintf('Original Image in Figure 1\n');
bpdq_show_im(im,drange,1);
title('Original Image');

figure(2)
fprintf('BPDQ_%g Reconstruction in Figure 2\n', p);
bpdq_show_im(im_bpdq,drange,1);
title(sprintf('bpdq-tv (p=%g) reconstruction, SNR %g dB',p,SNR_bpdq));
drawnow;

figure(3)
fprintf('BPDN Reconstruction in Figure 3\n', p);
bpdq_show_im(im_bpdn,drange,1);
title(sprintf('bpdn-tv reconstruction, SNR %g dB',SNR_bpdn));
drawnow;

figure(4)
fprintf('Convergence Analysis in Figure 4\n');
subplot(1,2,1)
plot(log10(D_bpdq.dr_relerr_save));
title('DR convergence (for bpdq)');
xlabel('iteration');
ylabel('log relative error');

subplot(1,2,2)
plot(log10(D_bpdn.dr_relerr_save));
title('DR convergence (for bpdn)');
xlabel('iteration')
ylabel('log relative error');

% The BPDQ Toolbox is free software: you can redistribute it and/or modify
% it under the terms of the GNU General Public License as published by
% the Free Software Foundation, either version 3 of the License, or
% (at your option) any later version.
%
% The BPDQ Toolbox is distributed in the hope that it will be useful,
% but WITHOUT ANY WARRANTY; without even the implied warranty of
% MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
% GNU General Public License for more details.
%
% You should have received a copy of the GNU General Public License
% along with The BPDQ Toolbox.  If not, see <http://www.gnu.org/licenses/>.

Displaying results and convergence curves
Original Image in Figure 1
BPDQ_10 Reconstruction in Figure 2
BPDN Reconstruction in Figure 3
Convergence Analysis in Figure 4

Published with MATLAB® 7.5