Coupling by diffusion : real model

We consider the following simple real model of phase oscillator coupled by diffusion. Each cell i has an internal phase oscillator :

$latex \displaystyle{d/dt ~\theta_i = \omega_i + ~f(A(x,t), ...)}$

Where f is the forcing signal depending on the protein A.

The protein A is produced by each cell and is propagated by diffusion :

$latex \displaystyle{d/dt ~A(x,t) = \alpha \sum_i \delta(x-x_i) g(\theta_i) ~-\gamma A(x,t) + ~D~d^2/dx^2 ~ A(x,t)}$ 

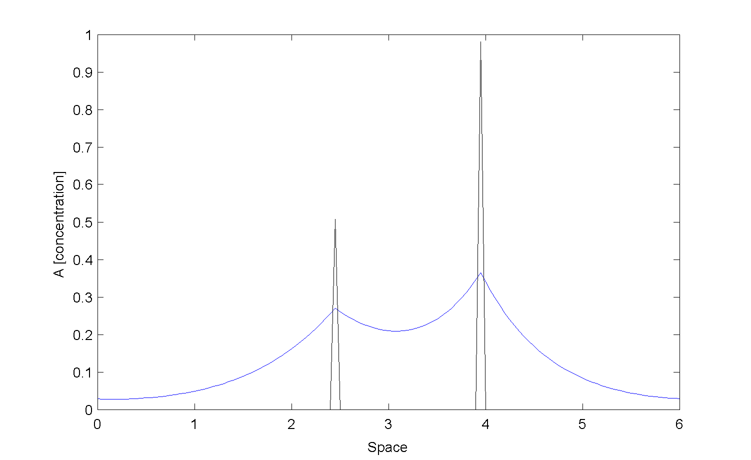
In this context how can the cell 1 read the phase of cell 2 ? The problem is that the signal emitted by cell 2 is masked by the one emitted by

cell 1.

One solution is the make the hypothesis that each cell has an internal representation of its own signal such that by comparison with the external signal A(x,t) it

can estimate the part of the signal coming form other cells. A way to implement this for the cell is to have another protein $latex \displaystyle{ B_i(t)  }$ :

$latex \displaystyle{d/dt~ B_i(t) = \alpha g(\theta_i) ~ -\gamma_B ~B_i(t) }$

Typically this protein is under the control of the same promoter than protein A but is not exported. Its degradation rate has also to be tuned.

Then the forcing signal f is given by $latex \displaystyle{ f = \beta * ( A(x_i,t) - B_i(t) ) }$

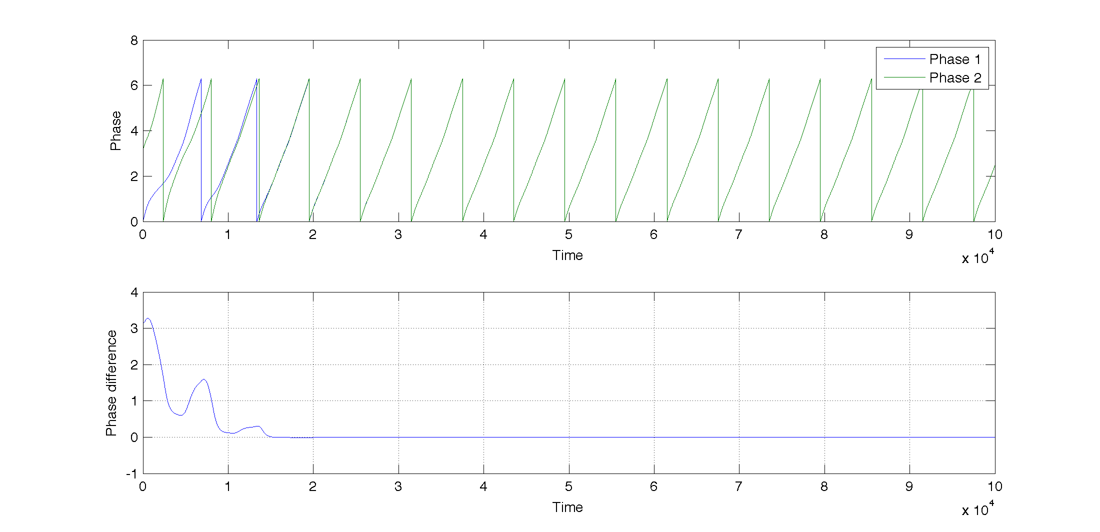
Results

Synchronization of two oscillators. Both intrinsic frequencies are equal. Initial phase difference is pi. 

For a certain set of parameters synchronization can occur in this context :

Synchronization of two noisy oscillators : 

$latex \displaystyle{d/dt ~\theta_i = \omega_i  + \eta(0,\sigma^2) + ~f(A(x,t), ...)}$

Synchronization of two oscillators with different intrinsic frequencies : 

$latex \omega_1 = 1, \omega_2 = 1.1 $ : 

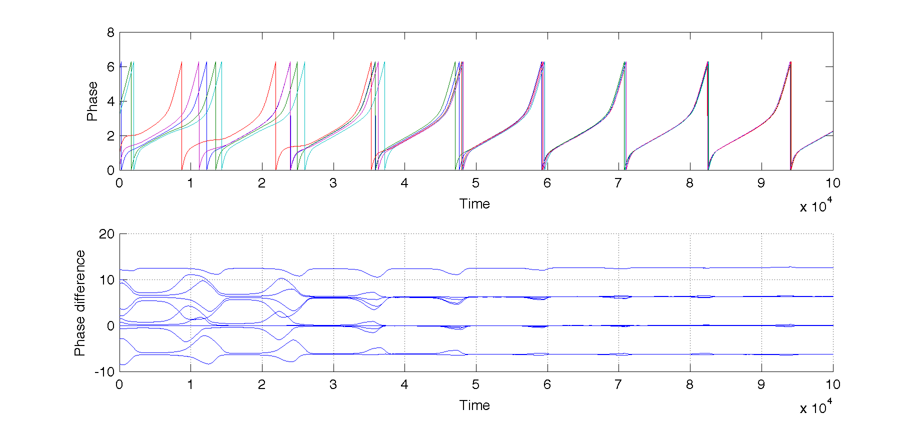
Synchronization of five equally spaced oscillators :