Coupling by diffusion : complex model

$latex \displaystyle{ \Large   }$

Complex field without diffusion (I) :

$latex \displaystyle{ \Large A_t = I(t) ~-\gamma A }$ 

If $latex \displaystyle{ \Large I(t) = \alpha e^{i f t} }$ then $latex\displaystyle{ \Large A(t) = \frac{\alpha}{if + \gamma} e^{i f t} }$ (initial condition ?)

With $latex \displaystyle{ \Large | \frac{\alpha}{if + \gamma}| = \frac{\alpha}{\sqrt{ f^2 + \gamma^2 } } }$ and $latex \displaystyle{ \Large   arg(\frac{\alpha}{if + \gamma}) = -arctan(f/\gamma )}$

If $latex \displaystyle{ \Large  \gamma = 0 }$  (long life time) then $latex \displaystyle{ \Large arg(\frac{\alpha}{if + \gamma}) = - \pi/2   }$

If $latex \displaystyle{ \Large  \gamma = +\infty }$ (short life time) then $latex \displaystyle{ \Large arg(\frac{\alpha}{if + \gamma}) = 0  }$

Then A(t) can be written as $latex \displaystyle{ \Large  \frac{\alpha}{\sqrt{ f^2 + \gamma^2 } } e^{- i ~arctan(f/\gamma )} e^{i f t}  = \frac{\alpha}{\sqrt{ f^2 + \gamma^2 } }\left( \cos(atan(f/\gamma)) -i~atan( \sin(f/\gamma) \right)  e^{i f t}  = \frac{\alpha}{\sqrt{ f^2 + \gamma^2 } } \left( \frac{1}{\sqrt { 1 + f^2/\gamma^2 } } - i~\frac{f/ \gamma  }{\sqrt{1 + f^2/\gamma^2 } } \right) e^{i f t} = \left( \frac{\gamma}{ \gamma^2 + f^2} - i~\frac{f}{\gamma^2 + f^2} \right) \alpha e^{i f t}     }$

Complex oscillator coupled with a complex field without diffusion (II) :

(1) $latex \displaystyle{ \Large z_t = (\mu +i \omega) z - z |z|^2 + A(t)   }$  

(2) $latex \displaystyle{ \Large A_t = \alpha z(t) ~-\gamma A }$  

Let's suppose that $latex \displaystyle{ \Large  z(t) = \beta e^{i \theta t} }$ then from (I) : $latex \displaystyle{ \Large A(t) = \frac{\alpha }{i\theta + \gamma} z(t)   }$

1. become :

$latex \displaystyle{ \Large i \theta z = (\mu +i \omega) z - \beta^2 z +  \frac{\alpha }{i\theta + \gamma} z  }$,

$latex \displaystyle{ \Large i \theta  = (\mu +i \omega)  - \beta^2  +  \frac{\alpha }{i\theta + \gamma}  = (\mu +i \omega)  - \beta^2  +  \alpha \frac{\gamma }{\theta^2 + \gamma^2} - i \alpha \frac{\theta }{\theta^2 + \gamma^2}  }$ 

Then :

(3) $latex \displaystyle{ \Large \beta = \sqrt { \mu + \alpha \frac{\gamma }{\theta^2 + \gamma^2} } }$ 

(4) $latex \displaystyle{ \Large \theta = \omega - \alpha \frac{\theta }{\theta^2 + \gamma^2 }} $  

The function $latex \displaystyle{ \Large \alpha \frac{\gamma }{\theta^2 + \gamma^2}  }$ as a maximum at $latex \displaystyle{ \Large \theta = \gamma   }$.

(4) gives the cubic equation : $latex \displaystyle{ \Large \theta^3 -\theta^2 \omega + \theta( \gamma^2 + \alpha ) - \omega \gamma^2   }$

If $latex \displaystyle{ \Large \gamma^2 >> \alpha }$ then $latex \displaystyle{ \Large \theta = \omega }$ (no effect of the coupling)

One can find the roots of this equations, in our case the first root is usually real and positive. 

Here is the relationship between the field amplitude $latex \displaystyle{\Large \alpha }$ and the resulting oscillator frequency $latex \displaystyle{ \Large \theta }$ using $latex \displaystyle{ \Large \gamma = 10, \omega = 5 ~and~ \mu = 2 }$ (the complex field as a phase shift of 0.46), using both the first root of the equation above and the measured frequency from ODE simulation of the system :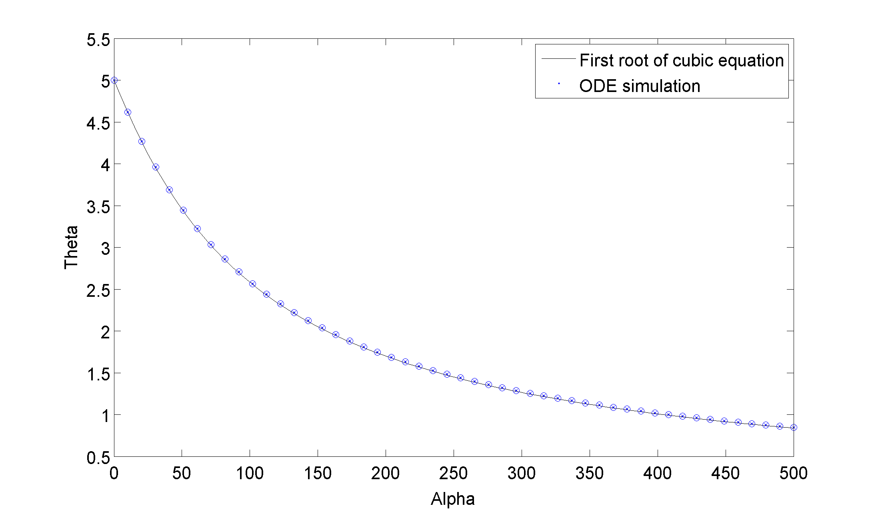

 

As the two methods match well, the above derivation is probably correct. 

Complex oscillator coupled with a complex field, a forcing phase and without diffusion (III) : 

(5) $latex \displaystyle{ \Large z_t = (\mu +i \omega) z - z |z|^2 + e^{i \Omega} A(t)   }$  

(6) $latex \displaystyle{ \Large A_t = \alpha z(t) ~-\gamma A }$

From (II) :

$latex \displaystyle{ \Large i \theta  = (\mu +i \omega)  - \beta^2  +  \frac{\alpha }{i\theta + \gamma}  = (\mu +i \omega)  - \beta^2  +  \alpha e^{i \Omega}\left(  \frac{\gamma }{\theta^2 + \gamma^2} - i \frac{\theta }{\theta^2 + \gamma^2}\right )  }$, we find :

(7) $latex \displaystyle{ \Large \beta^2 =  \mu + \frac{\alpha }{ \theta^2 + \gamma^2} \left ( \cos(\Omega) \gamma + \sin(\Omega) \theta \right) = \mu + \frac{\alpha }{\sqrt{\theta^2 + \gamma^2 }}\left ( \cos(\Omega - atan(\theta / \gamma)) \right) }$ 

(8) $latex \displaystyle{ \Large \theta = \omega - \frac{\alpha }{\theta^2 + \gamma^2 }\left ( \sin(\Omega) \gamma  - \cos(\Omega) \theta \right)  = \omega - \frac{\alpha }{\sqrt{\theta^2 + \gamma^2 }}\left ( \sin(\Omega - atan(\theta / \gamma)) \right) }$  

(8) gives the cubic equation : $latex \displaystyle{ \Large \theta^3 -\theta^2 \omega + \theta( \gamma^2 + \alpha \cos(\Omega) ) - \omega \gamma^2  - \alpha \gamma \sin(\Omega) }$

One can easily show that if $latex \displaystyle{ \Large \Omega = atan(\omega / \gamma) }$ then $latex \displaystyle{ \Large \theta = \omega }$ is a solution of (8).

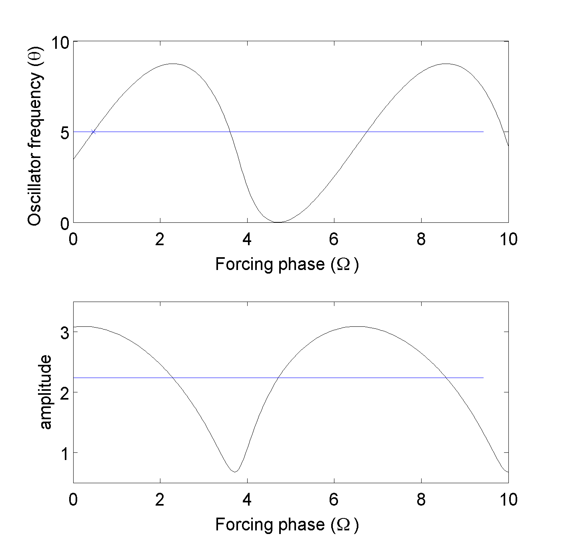
Then the first root of this equation is a periodic function of $latex \displaystyle{\Omega}$ ( $latex \displaystyle{ \Large \gamma = 10, \omega = 5 ~and~ \alpha = 50, \mu = 5 }$ )