|
Navigation
|
aIn order to test the stability of trajectories for a given speed c we go into the moving frame (z,t) = (x-ct,t) $latex \displaystyle{ \Large w_t = \alpha_w \frac{w^2}{1 + w^2} - \gamma_{vw} ~ v \frac{w}{k + w} - \lambda_w ~w + A + c w_z}$ $latex \displaystyle{ \Large v_t = \frac{w^2}{1 + w^2} - v + c v_z}$ $latex \displaystyle{ \Large A_t = \alpha_A w - \lambda_A~ A + D_A~A_{zz} + c A_z} $
In order to linearize the system around a particular solution, we compute the Jacobian : $latex \displaystyle{ \Large F_U~(~Q(z)~) = \left[ \begin {array}{ccc} 2\,{\frac {{\it \alpha_w}\,w}{1+{w}^{2}}}-2\,{\frac {{\it \alpha_w}\,{w}^{3}}{ \left( 1+{w}^{2} \right) ^{2}}}-{\frac {{\it \gamma_{vw} }\,v}{k+w}}+{\frac {{\it \gamma_{vw} }\,wv}{ \left( k+w \right) ^{2}}}-{\it \lambda_v}&-{\frac {{\it \gamma_{vw} }\,w}{k+w}}&1\\\noalign{\medskip}2\,{\frac {w}{1+{w}^{2}}}-2\,{\frac {{w}^{3}}{ \left( 1+{w}^{2} \right) ^{2}}}&-1&0\\\noalign{\medskip}{\it \alpha_A}&0&-{\it \lambda_A}\end {array} \right] }$
Then the linearized differential operator is : $latex \displaystyle{ \Large L = D~\partial_{zz} + C~\partial_z + F_U~(~Q(z)~) }$
With $latex \displaystyle{ \Large D = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & D_A \end{pmatrix} }$ and $latex \displaystyle{ \Large C = \begin{pmatrix} c & 0 & 0 \\ 0 & c & 0 \\ 0 & 0 & c \end{pmatrix} }$
The eigenfunctions of the operator $latex \displaystyle{ \Large L = D~\partial_{zz} + C~\partial_z }$ are :
$latex \displaystyle{ \Large U = (u_1, u_2, u_3)^T = (~e^{ikx}, 0, 0)^T, ~\lambda = c ik }$ $latex \displaystyle{ \Large U = (u_1, u_2, u_3)^T = (0, e^{ikx}, 0)^T, ~\lambda = c ik }$ $latex \displaystyle{ \Large U = (u_1, u_2, u_3)^T = (0, 0, e^{ikx})^T, ~\lambda = c ik - D_A k^2 }$
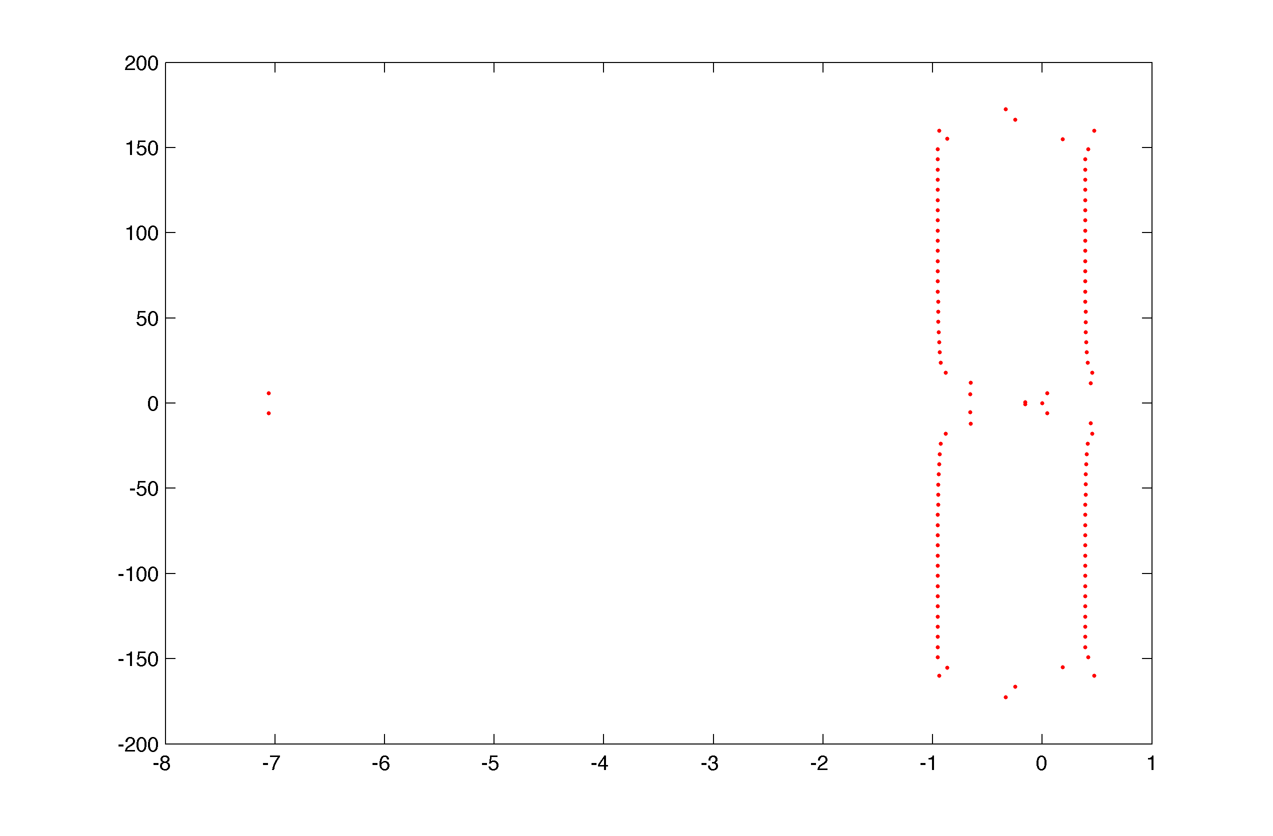
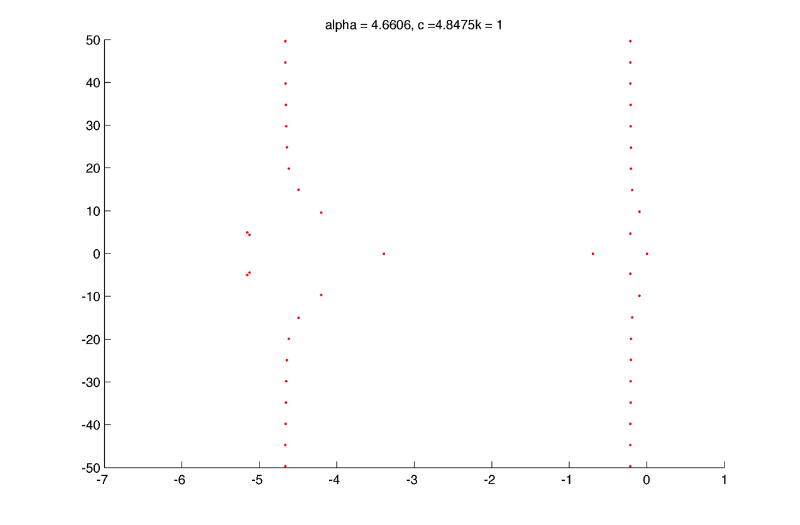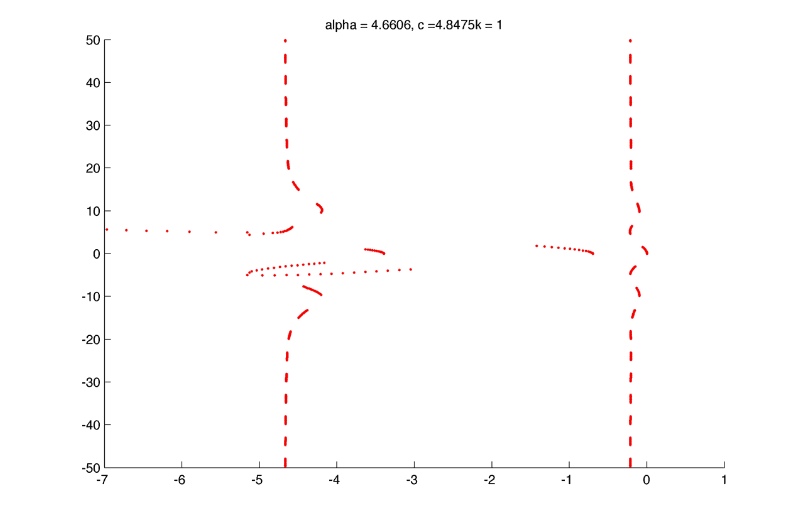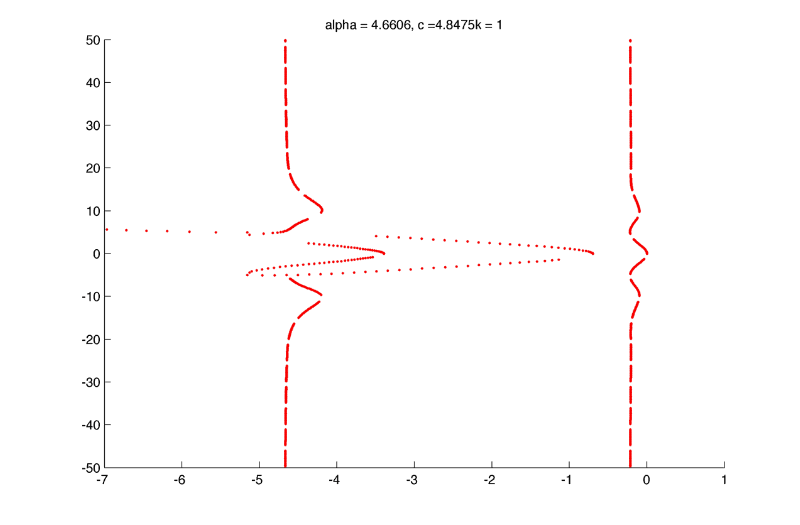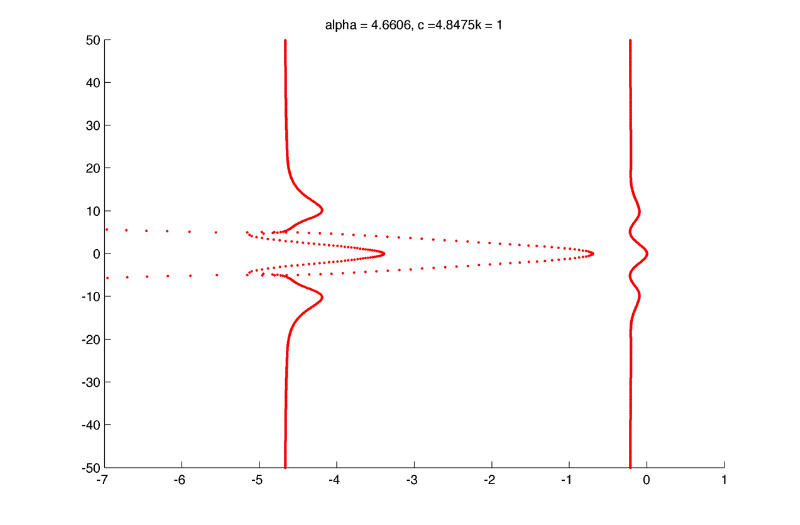
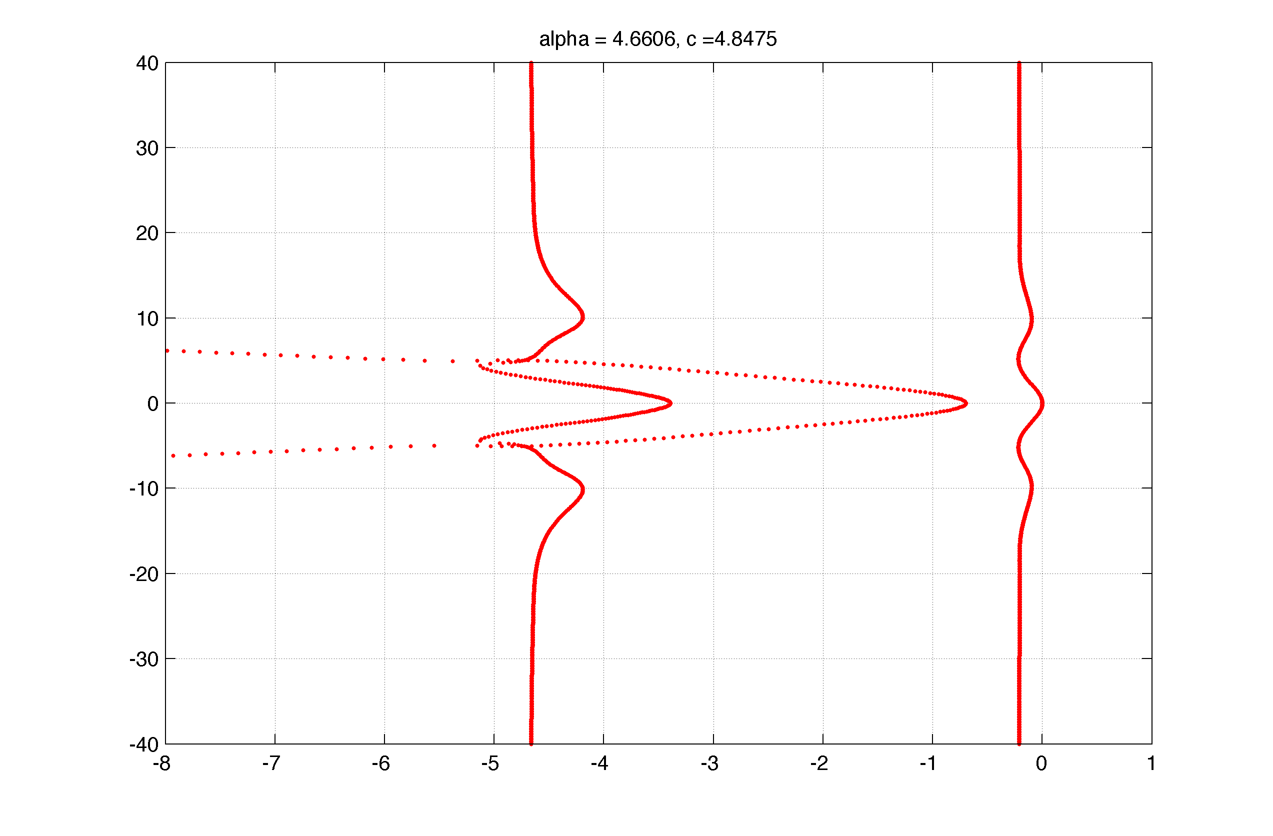
Thus the spectrum is composed of two vertical lines and one quadratic curve in the complex plane. Theses curves seems to shift along the real axis when the Jacobian part corresponding to homogenous solution is added. For example
Rewriting the problem in Fourier space :
As the Jacobian is periodic in z with period T, Bloch's theorem state that the eigenfunctions of the differential operator can be written as : $latex \displaystyle{ \Large u(x) = e^{ikx} \sum_n c_n ~e^{ i n 2 \pi x / T} = \sum_n c_n ~ e^{ikx} ~e^{ i q_n x } }$ with $latex \displaystyle{ \Large k \in [0, 2 \pi / T]}$. Then the eigenvalue problem $latex \displaystyle{ \Large Lu = \lambda u }$ become :
$latex \displaystyle{ \Large \sum_n c_n \left( i c (q_n + k) - D (q_n + k)^2 + F_U~(~Q(z)~) \right ) e^{ i q_n x } = \lambda \sum_n c_n ~e^{ i q_n x } }$
Each side is T-periodic in x, so we compute its Fourier serie : $latex \displaystyle{ \Large G[m] = \frac{1}{T}\int_0^{T} g(x)\cdot e^{-i 2\pi \frac{m}{T} x}\, dx }$ :
$latex \displaystyle{ \Large \sum_n c_n \left( (i c (q_n + k) - D (q_n + k)^2) \delta_{m,~n} + \tilde{F}_U~(Q)[m - n ] \right ) = \lambda \sum_n c_n ~ \delta_{m, ~n} }$
$latex \displaystyle{ \Large c_m (i c (q_m + k) - D (q_m + k)^2) + \sum_n \tilde{F}_U~(Q)[m - n ] c_n = \lambda c_m }$ Truncating the sum it gives the eigenvalue problem :
$latex \displaystyle{ \Large \tilde{L} c = \lambda c }$
Here is the matrix $latex \displaystyle{ \Large \tilde{L} }$ for k=0 close to the Hopf bifurcation (log 10 scale) :
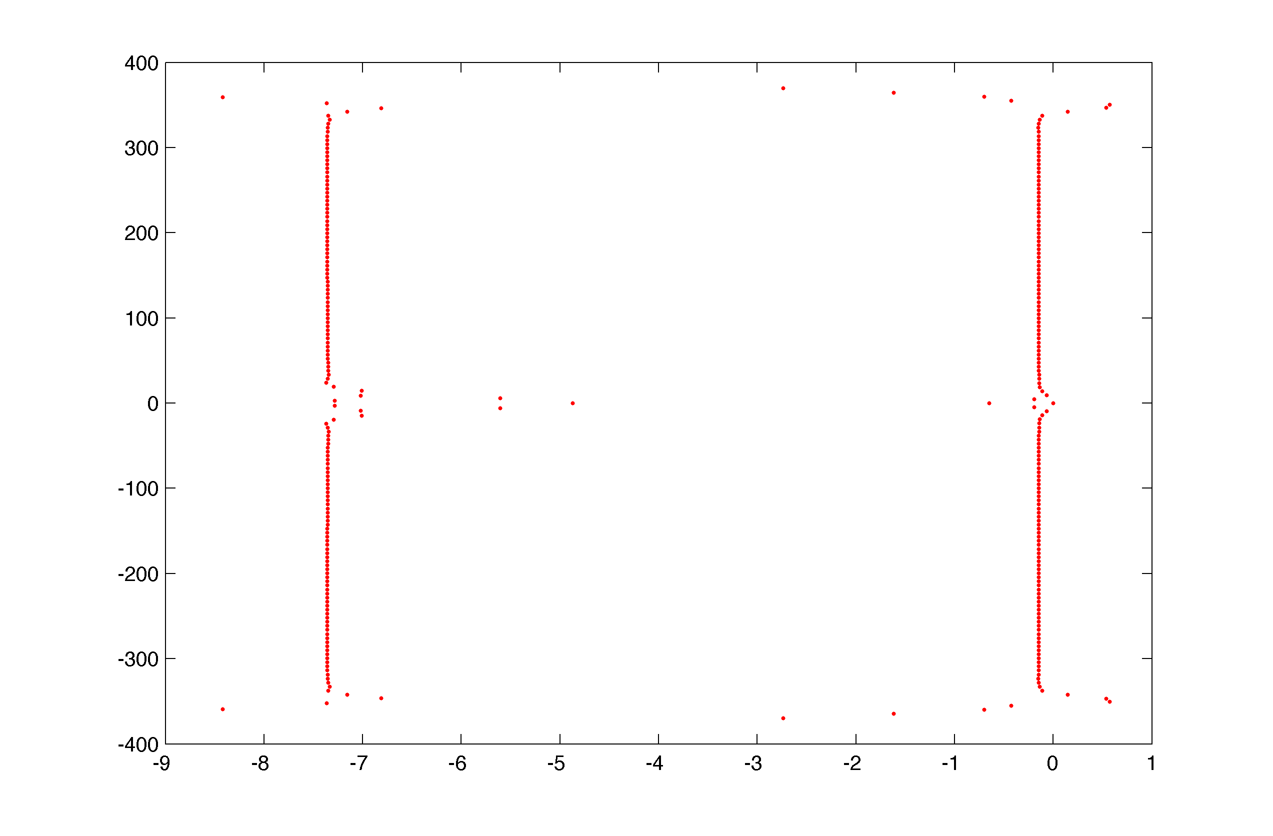
The top of the spectrum in the complex plane :
As in the homogenous case there is two vertical lines (one positive one negative) and a quadratic curve (going far in the negative values).
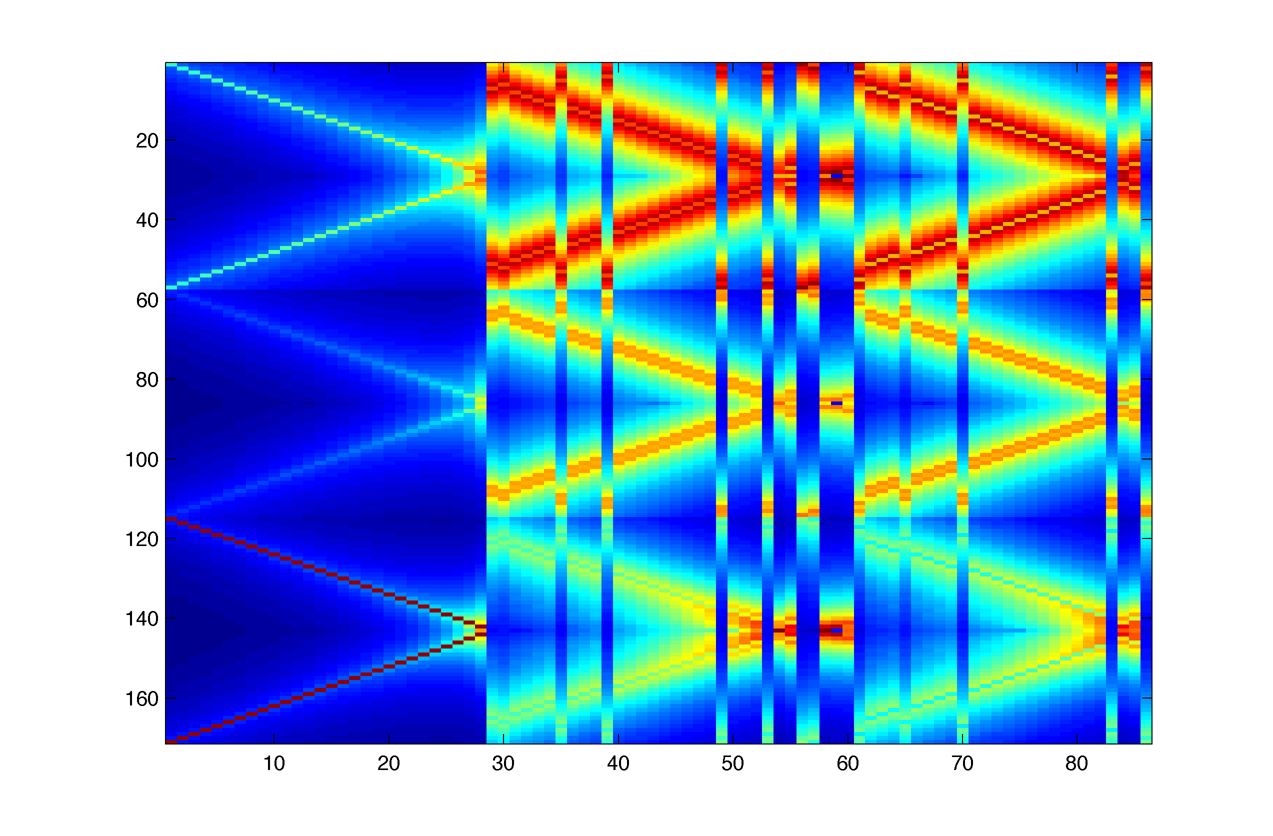
And the eigenfunctions, sorted by real part of eigenvalue (the first block is dominated by specie A and the two last one by w) :
Further from the hopf bifurcation, the two vertical lines are negative but some eigenvalues associated with high frequencies become positive :
Theses high frequencies eigenfunctions are likely to be numerical artifacts, in the plot above theses instabilities are about n = 150, but on the plot bellow the same frequencies are stable and the highest frequencies (~800) are unstable :
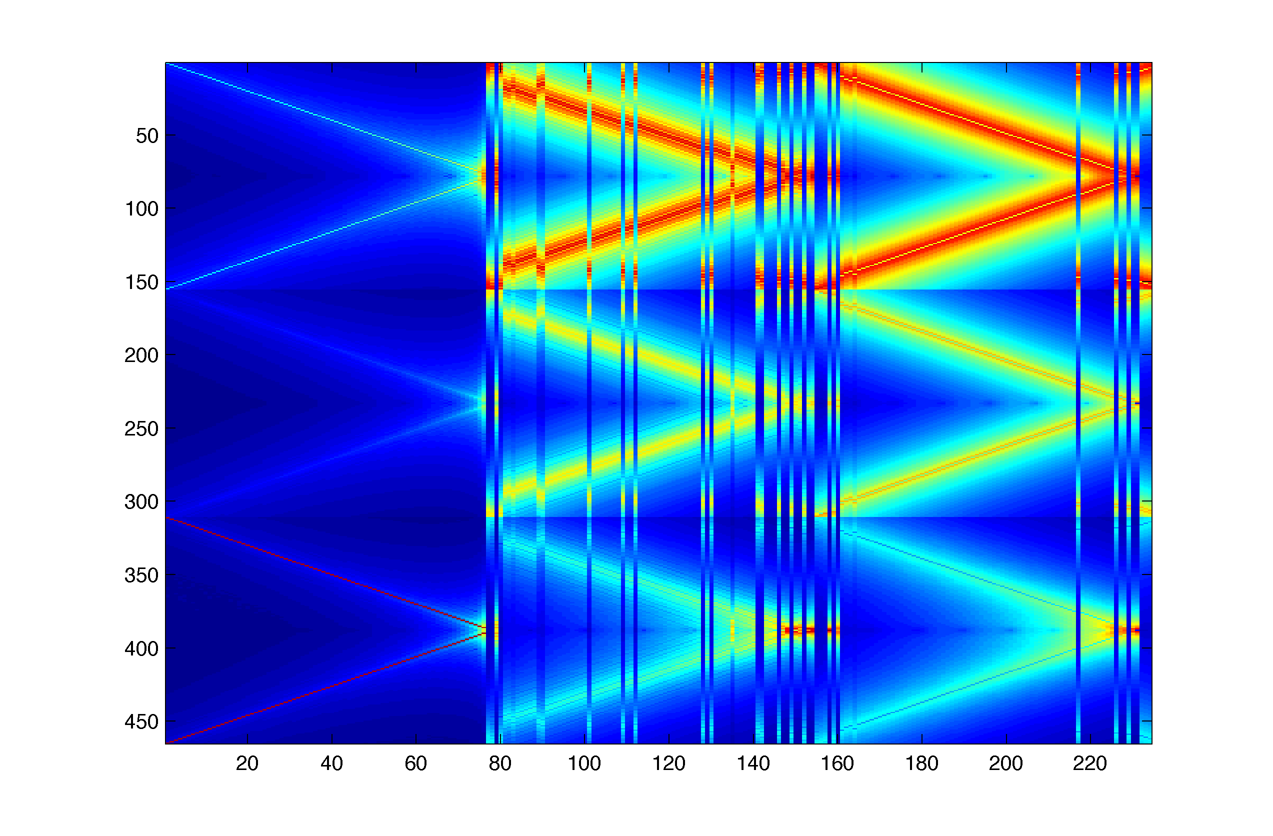
Spectrum while changing k from 0 to 1 :
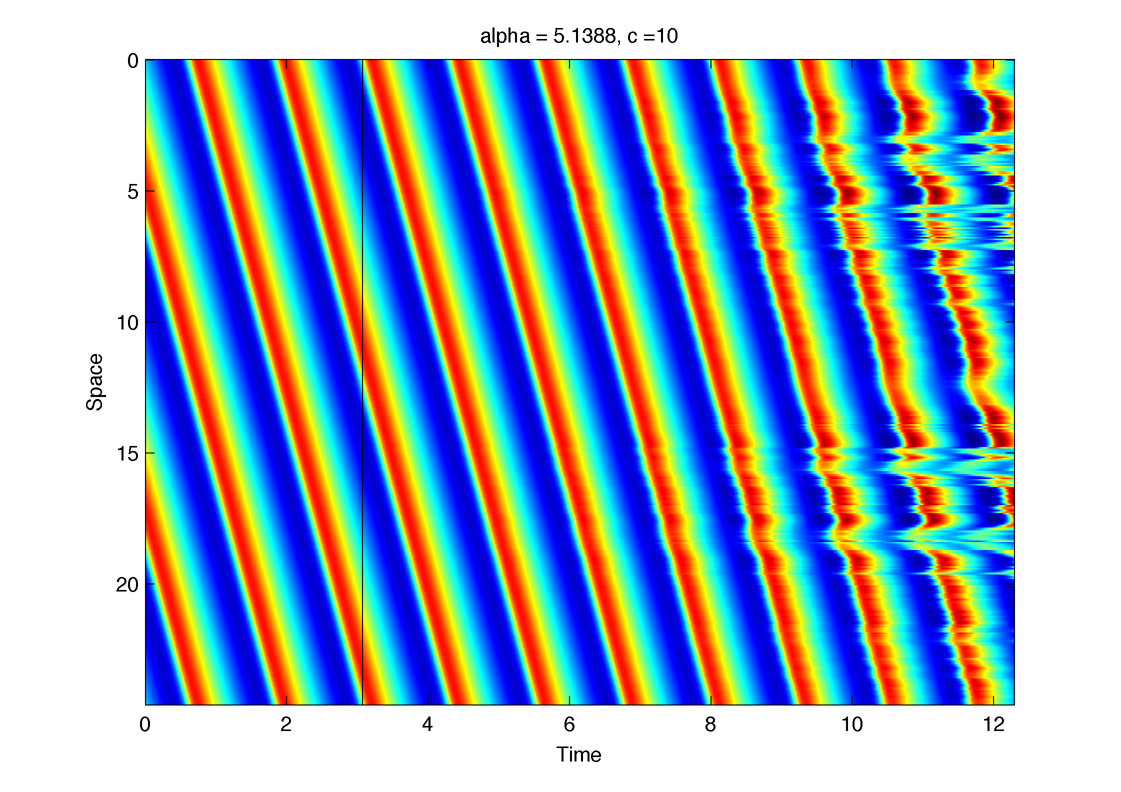
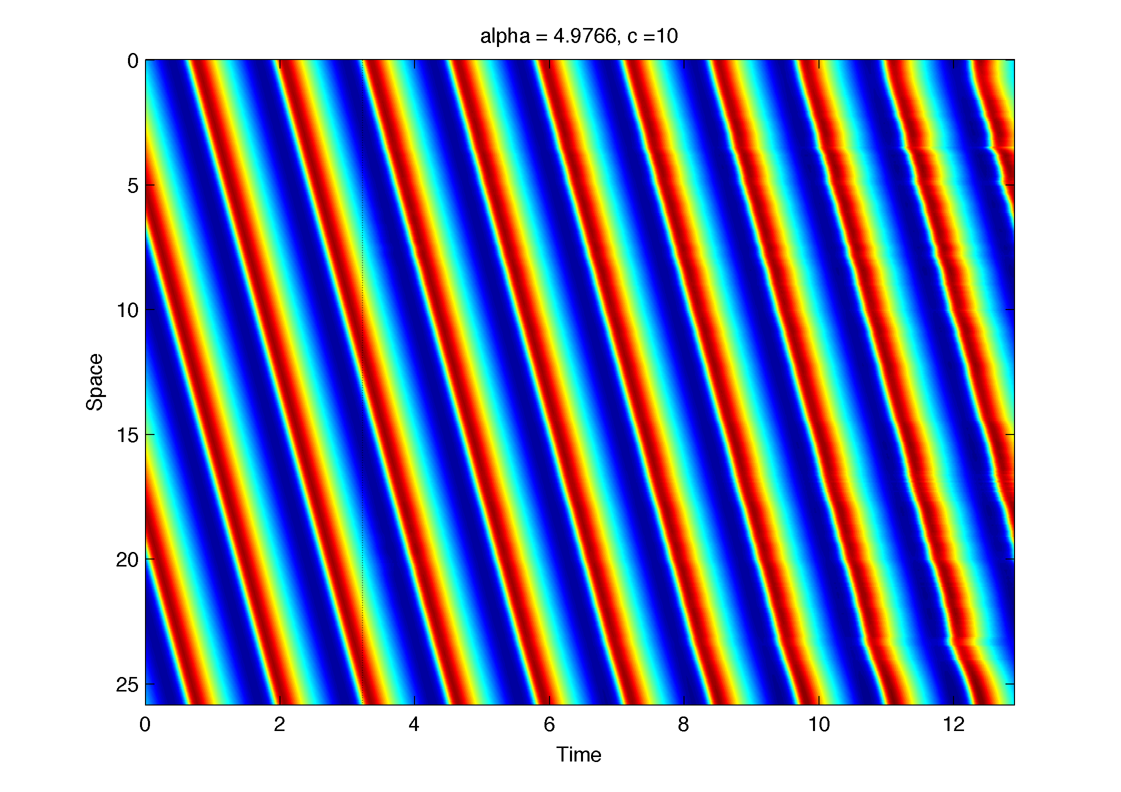
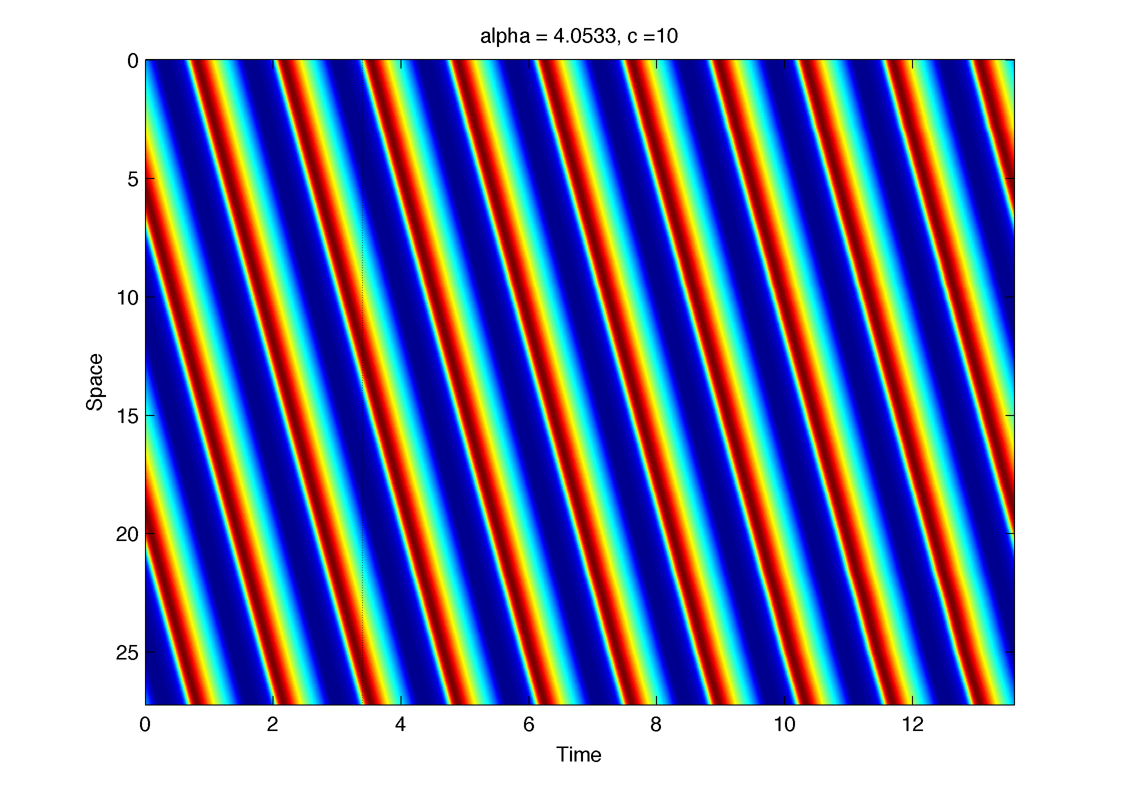
Measuring stability trough simulation ? A small perturbation is added a t = 3 :
Rewriting the problem in Fourier space (continuous) :
As the Jacobian is periodic in z with period T, Bloch's theorem state that the eigenfunctions of the differential operator can be written as : $latex \displaystyle{ \Large u(x) = e^{ikx} \sum_n c_n ~e^{ i n 2 \pi x / T} = \sum_n c_n ~e^{ i q_n x } }$ Then the eigenvalue problem $latex \displaystyle{ \Large Lu = \lambda u }$ become :
$latex \displaystyle{ \Large \sum_n c_n \left( i c q_n - D q_n^2 + F_U~(~Q(z)~) \right ) e^{ i q_n x } = \lambda \sum_n c_n ~e^{ i q_n x } }$
Taking the fourier transform on both side $latex \displaystyle{ \Large \int_{-\infty}^{\infty} f(x) e^{-i m x} dx }$
$latex \displaystyle{ \Large 2 \pi \sum_n c_n \left( (i c q_n - D q_n^2) \delta( m - q_n ) + \tilde{F}_U~(Q)(m - q_n ) \right ) = 2 \pi \lambda \sum_n c_n ~ \delta( m - q_n ) }$
|