Linear Phase Solutions

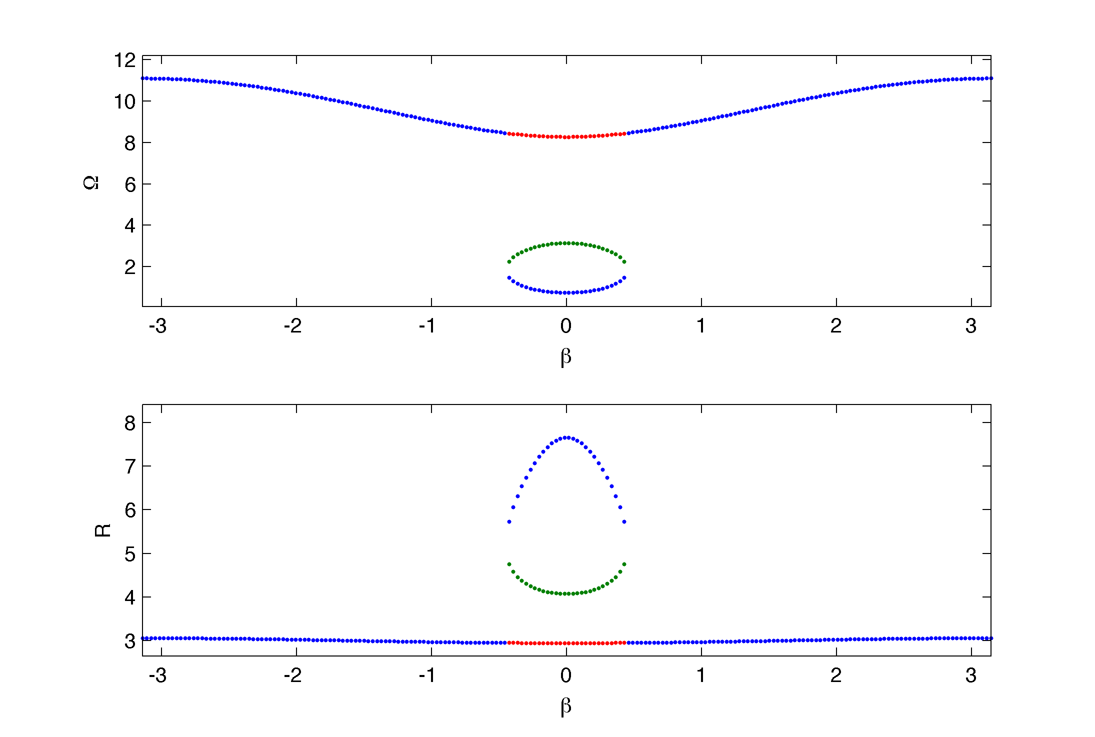
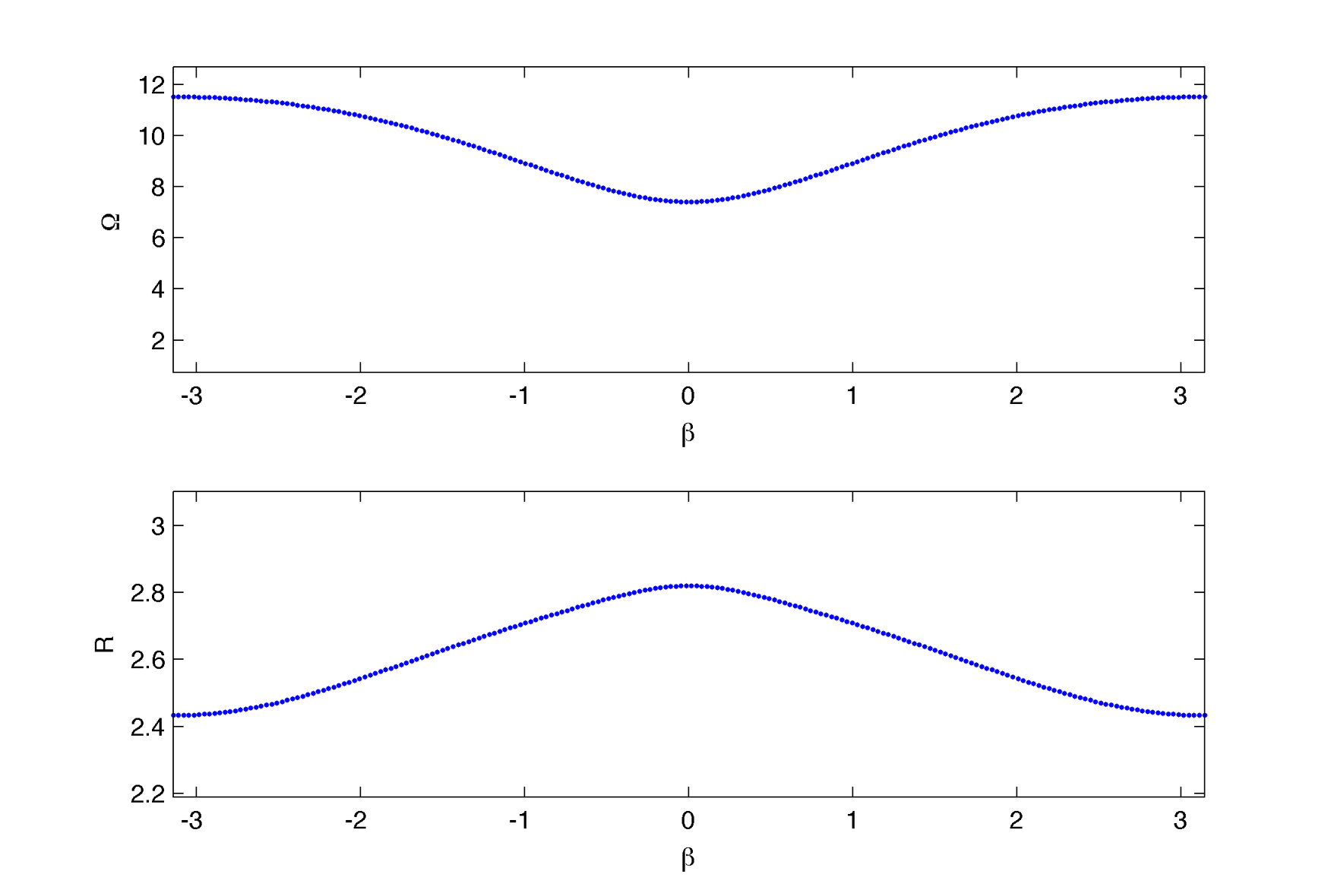
We consider solution of the type : $latex \displaystyle{ \Large z_j = R e^{i \Omega t + i \phi_j} }$ with  : $latex \displaystyle{ \Large \phi_j = \beta j }$

Then the self consitence equation for the collective frequency become :

$latex \displaystyle{ \Large \Omega = \omega +  \sum_{j=-N}^N  R_A( \Omega,|j| \Delta x)  \sin[ \theta_A(\Omega, |j| \Delta x)~ + ~\theta + \beta j]   } $ and do not depend anymore on $latex \displaystyle{ \Large R}$.

Parameters :

alpha = 50; gamma = 1/2; D = 1;  mu = 1; dx = 1; omega = 10;

0. Solutions :

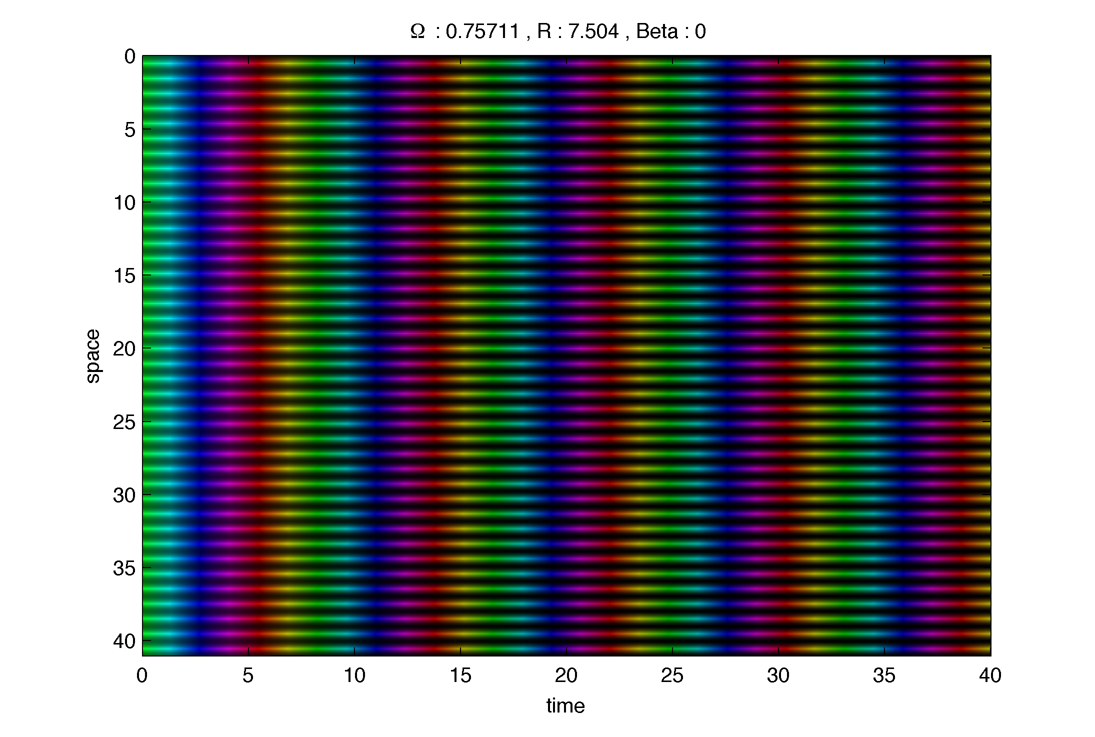
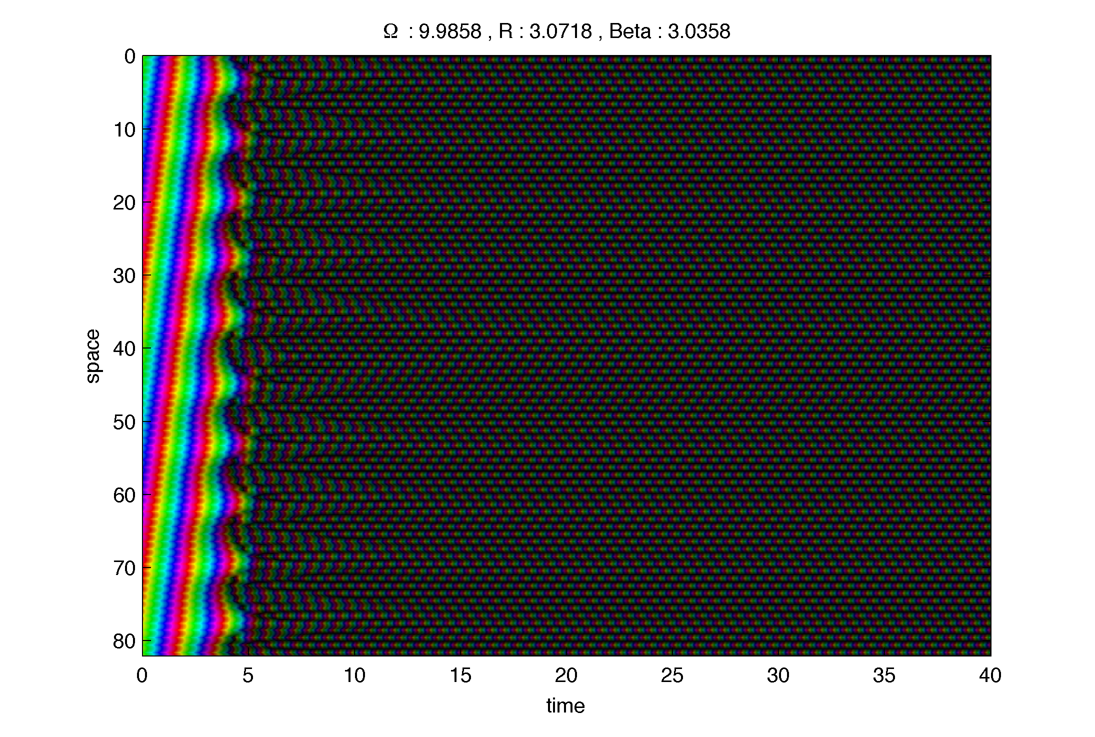
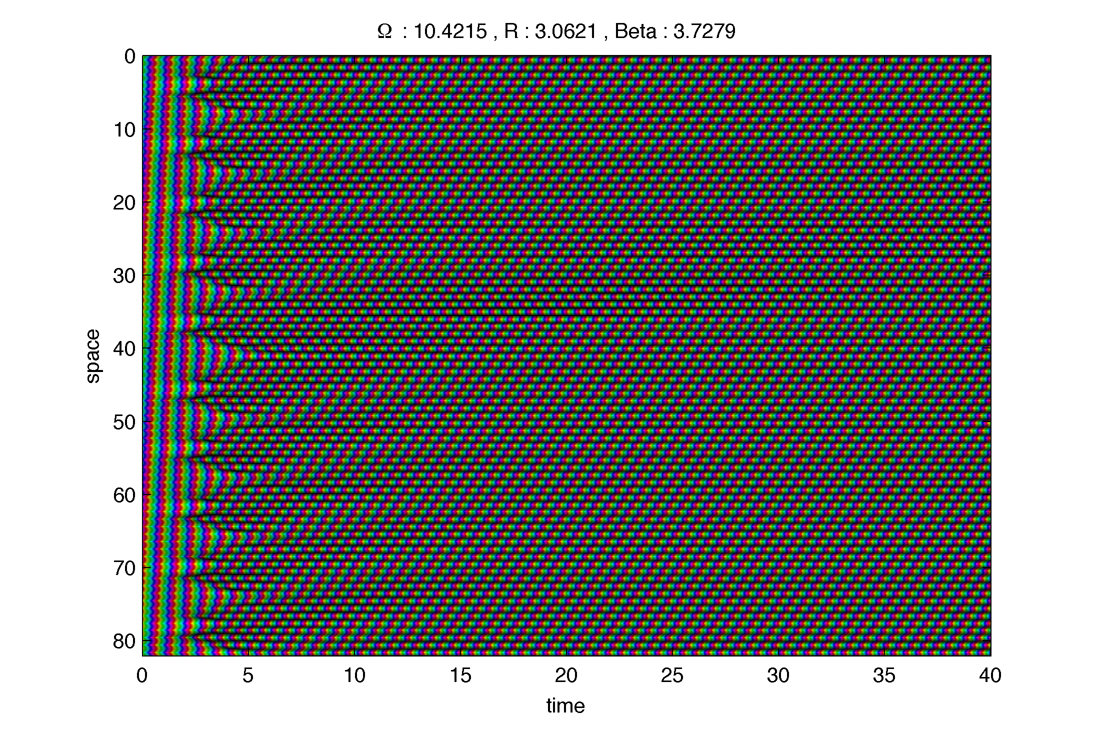
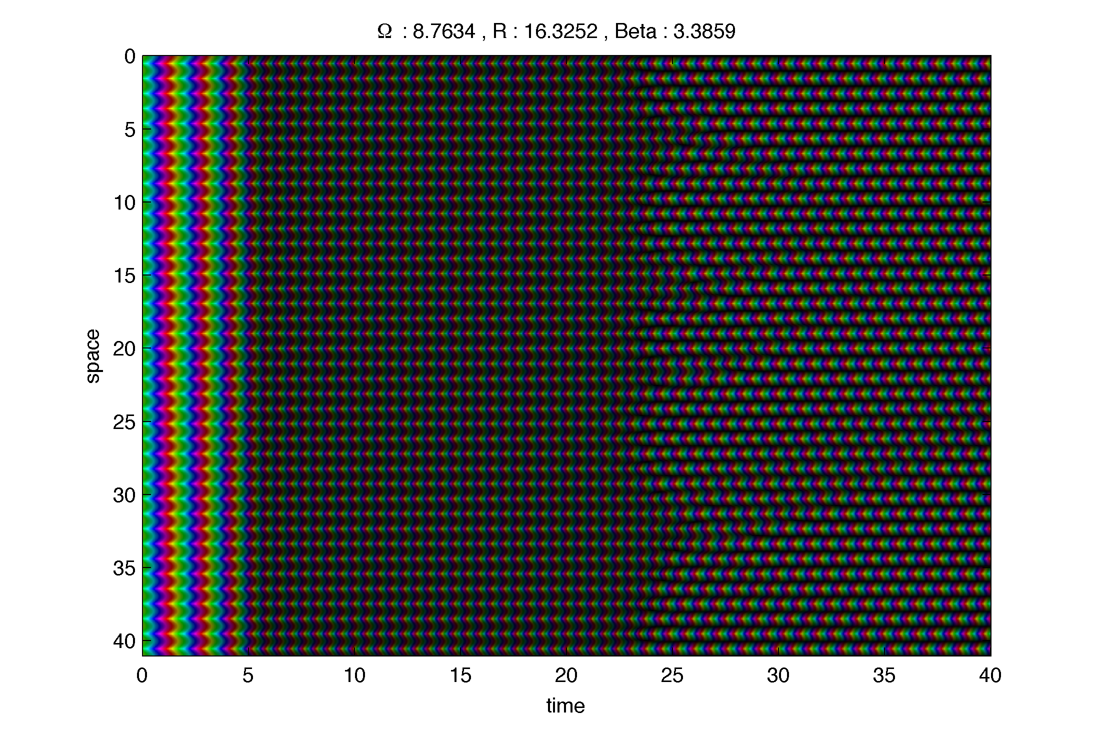
1. Ferromagnetic case : $latex \displaystyle{ \beta = 0 }$

Bottom one (blue), seem fairly stable :

Middle one, green. It rapidly degenerate in the top one and then into the antiferromagnetic solution :

Top one, red. It degenerate into the antiferromagnetic solution :

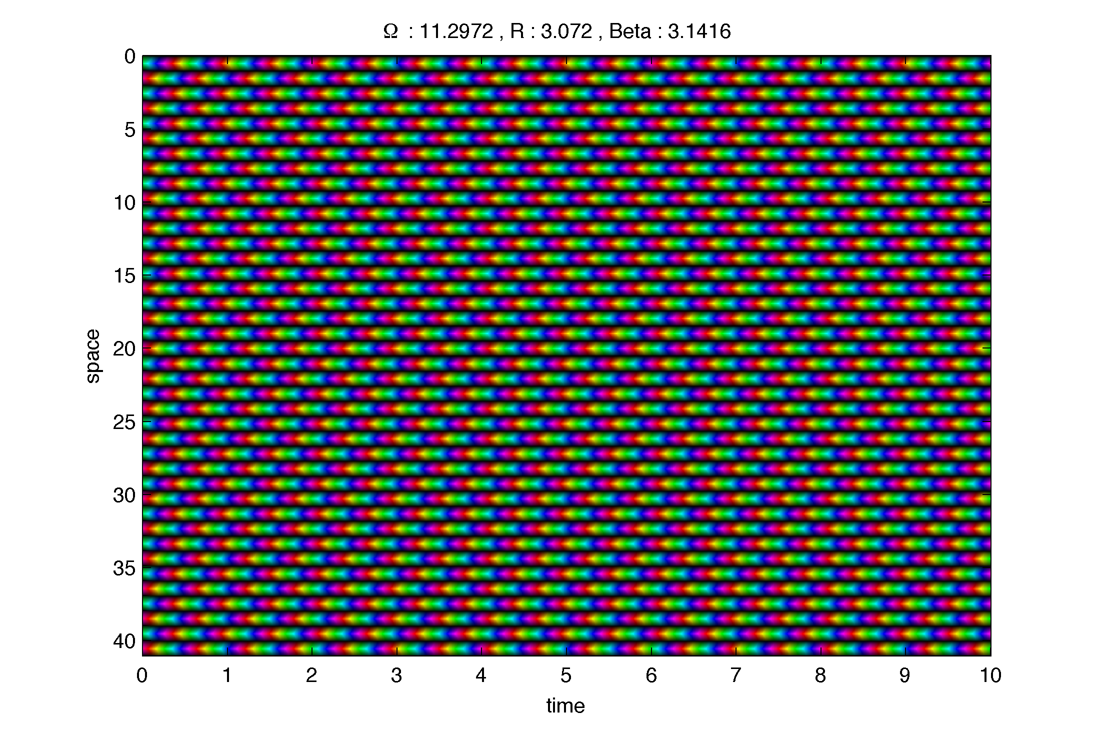
2. Antiferromagnetic case : $latex \displaystyle{ \beta = \pi }$

Seems to be very stable :

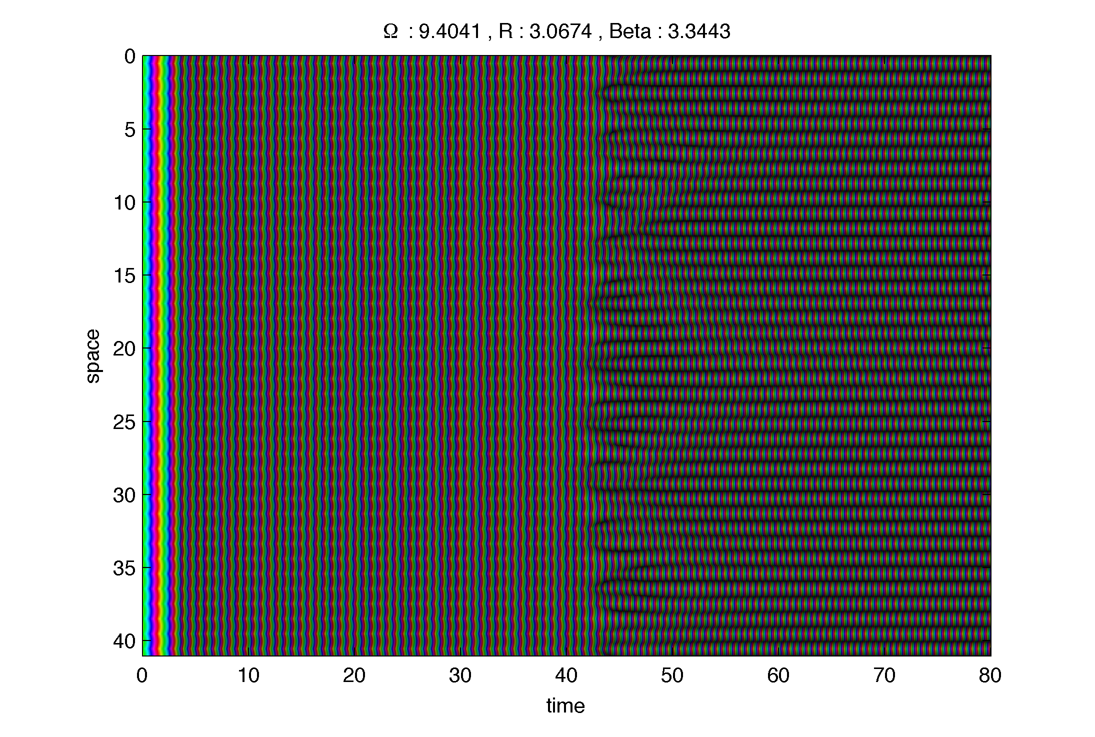
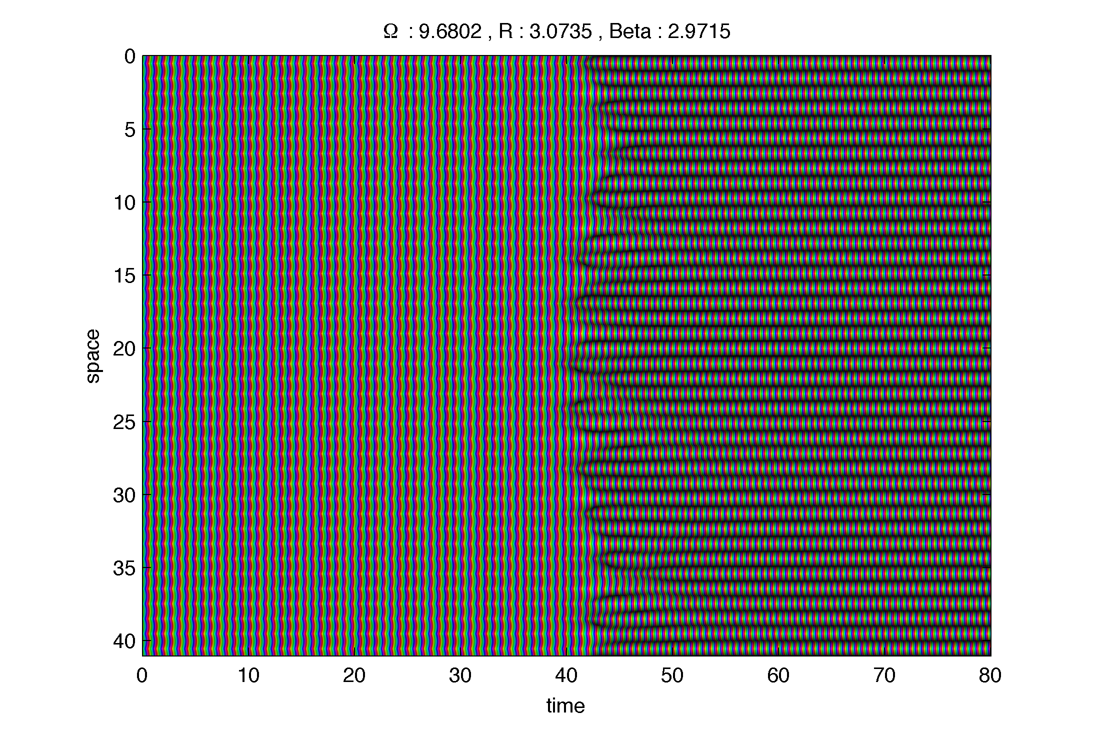
3. Intermediate case : $latex \displaystyle{ \beta =  0.1551}$

Different regim :

alpha = 800; gamma = 1; D = 0.3;  mu = 1; dx = 1; omega = 10;

1. Ferromagnetic case : $latex \displaystyle{ \beta = 0 }$

Bottom solution (blue) : seems stable.

Middle solution (green) : same behavior than previous regim :

Similar behavior : Except the bottom low frequency solution, everything seem to go on the antiferromagnetic solution. 

Chaotic regim :

alpha = 50; gamma = 2; D = 2; mu = 1; d = 1; omega = 10; 

High diffusion, high degradation rate : ferromagnetic solutions seems stable

alpha = 50; gamma = 10; D = 10;