mRNA Half-lives

From the supplement :

" Second, for the 254 ‘signature set’ genes, we compared the degradation rates estimated by the constant and varying degradation models with the rates we predicted based on the Actinomycin D data (Methods; Supplementary Fig. 12a-b). We find that the two are highly correlated, but that our models predict shorter RNA half-lives on average (i.e., higher degradation rate) than half-lives measured by Actinomycin D (e.g., median half- life at 0 hours is 26 min. with the ‘varying degradation’ model, and 80 min. with Actinomycin D). The inherited biases in standard Actinomycin D techniques may contribute to the observed discrepancies. "

 

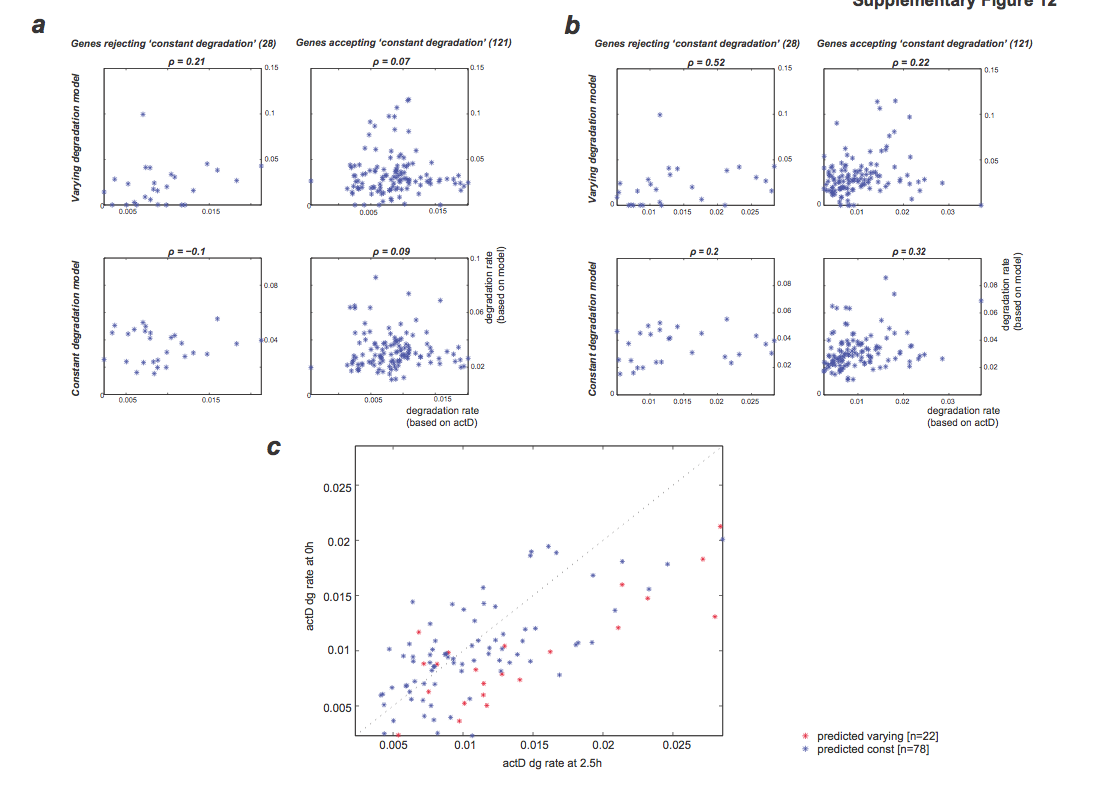
"Notably, this discrepancy in absolute degradation rates may be due to inherent limitations in all techniques (ours, which estimates degradation rates indirectly, as well as others, which are significantly biased), and highlight the need for direct and reliable methods to measure degradation rates. Yet, despite the possible discrepancy in the absolute degradation rates, the correlation with other rate estimates remains high, suggesting that the ranking of the RNAs stability and most importantly, the ratio between RNA transcription and degradation rates, on which we base our conclusions, are reliable and accurate."

Data for 10 minutes integration

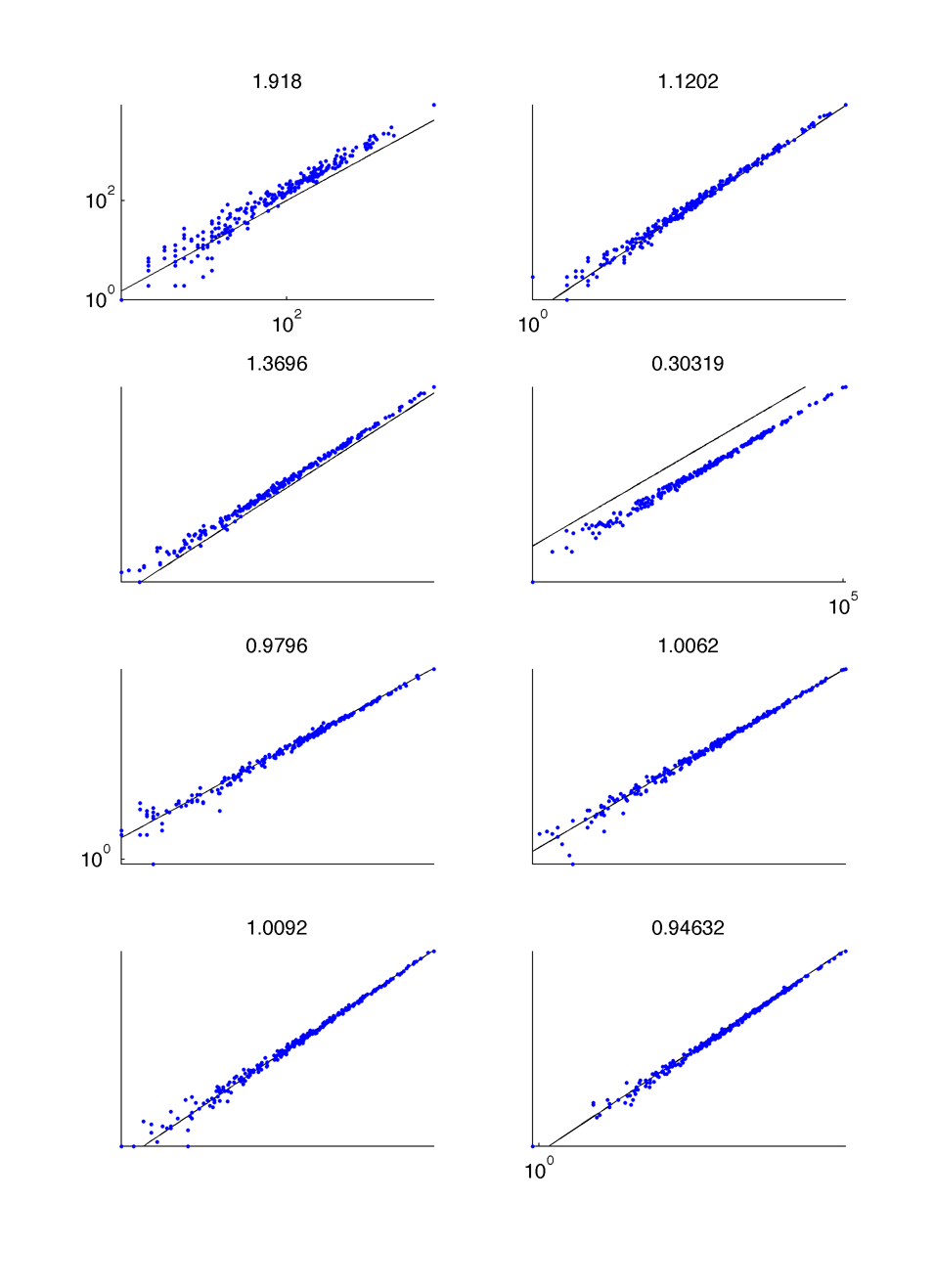
Replicates correlation with scaling factor in loglog :

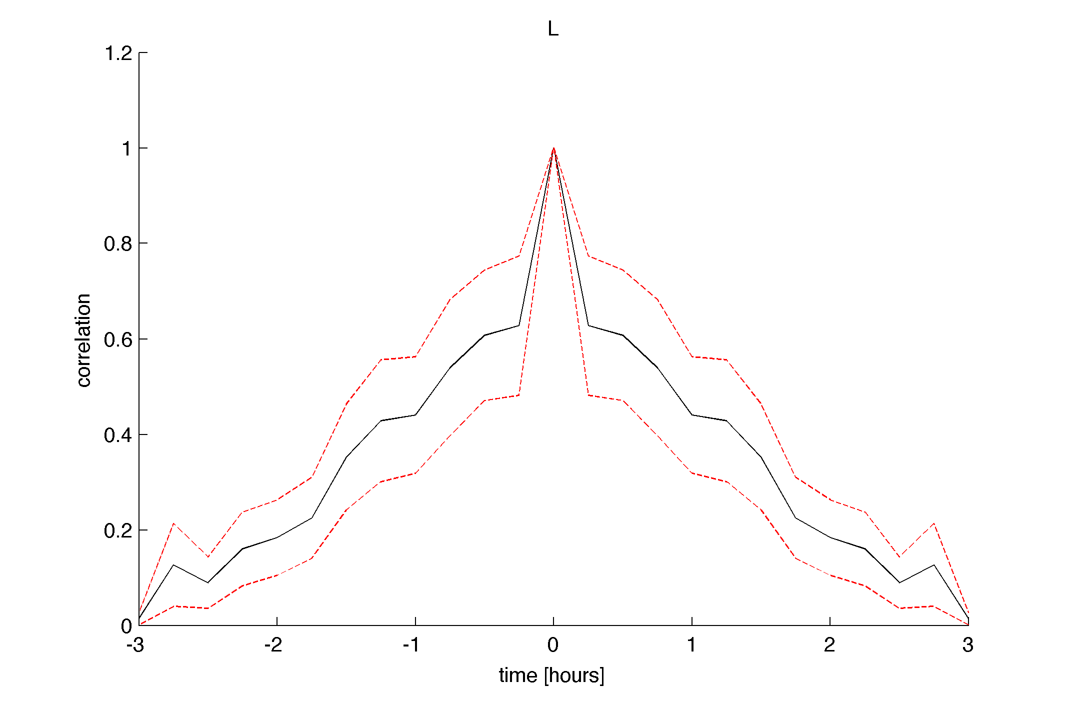
Time cross-correlation :

Model with constant production rate

For each gene i :

Model :

$latex \displaystyle{ \large \partial_t m_i = \alpha_i -\gamma_i m_i }$

For each gene i and time point j :

Data :

 $latex \displaystyle{ \large L_{ij} = c^L_j ~\int_{t_j}^{T+t_j}  \alpha_i -\gamma_i m_i(t) ~dt }$  

 $latex \displaystyle{ \large T_{ij} = c^T_j ~\int_{t_j}^{T+t_j} -\gamma_i m_i(t) ~dt }$

 $latex \displaystyle{ \large L_{ij} = c^L_j ~\frac{\alpha_i}{\gamma_i} ~ \left( 1- \exp(-\gamma_i T) \right) }$  

 $latex \displaystyle{ \large T_{ij} = c^T_j ~\frac{\alpha_i}{\gamma_i} ~ \exp(-\gamma_i T) }$

Model with 3 steps production rate

Fits are a bit better :

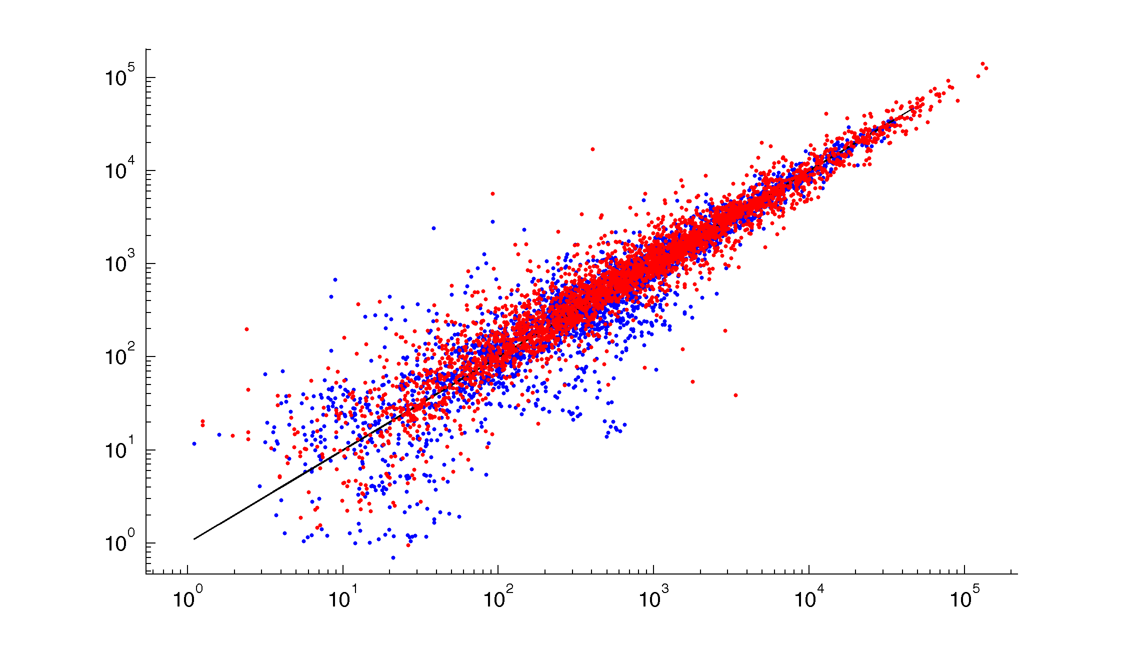
Half lives are a bit shorter : 1-2 hours.

But there is almost not correlation with the constant production rate model (mean is done on optimization runs) :
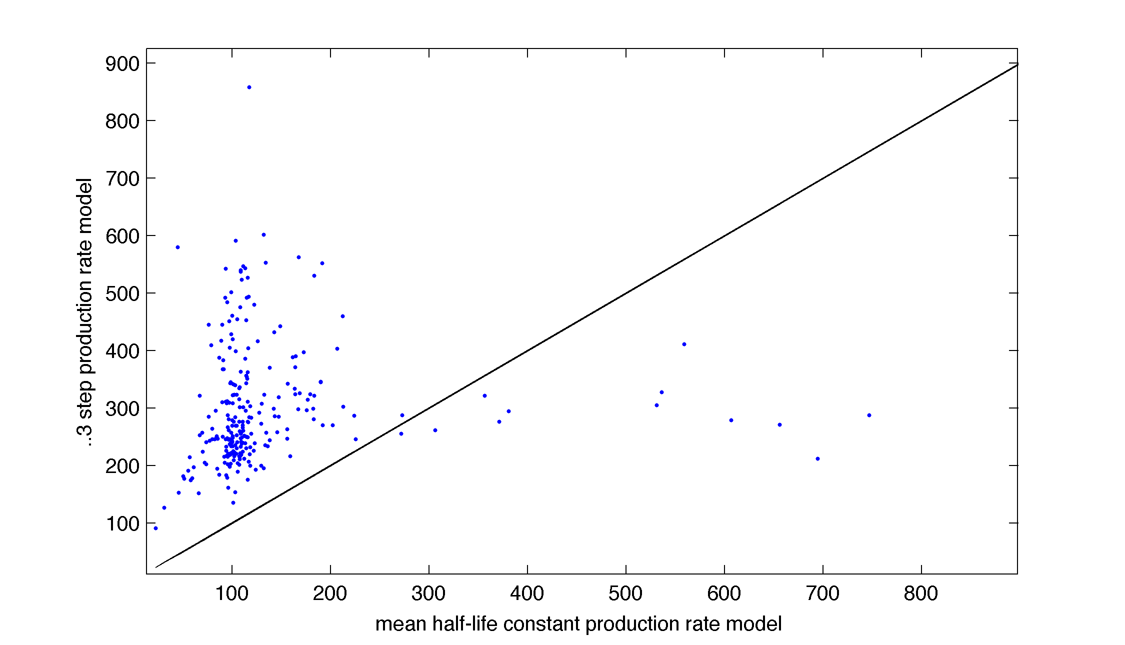