The model :

$latex \displaystyle{ \Large w_t = \alpha_w \frac{w^2}{1 + w^2} - \gamma_{vw} ~ v \frac{w}{k + w} - \lambda_w ~w + I}$

$latex \displaystyle{ \Large v_t = \frac{w^2}{1 + w^2} - v}$

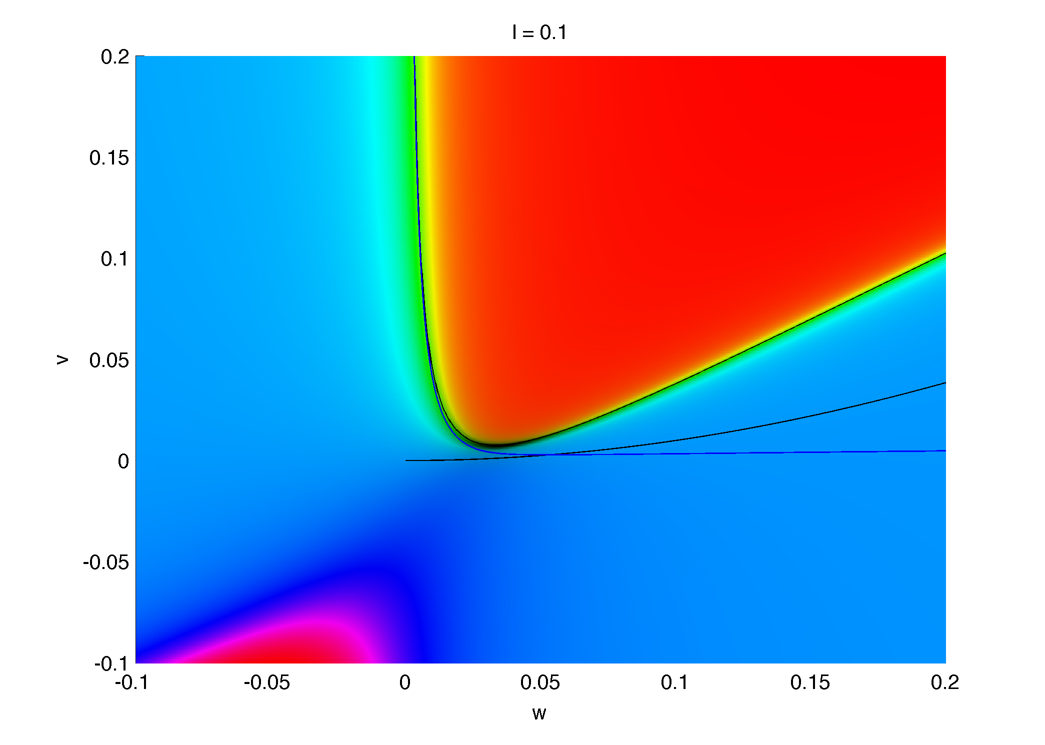
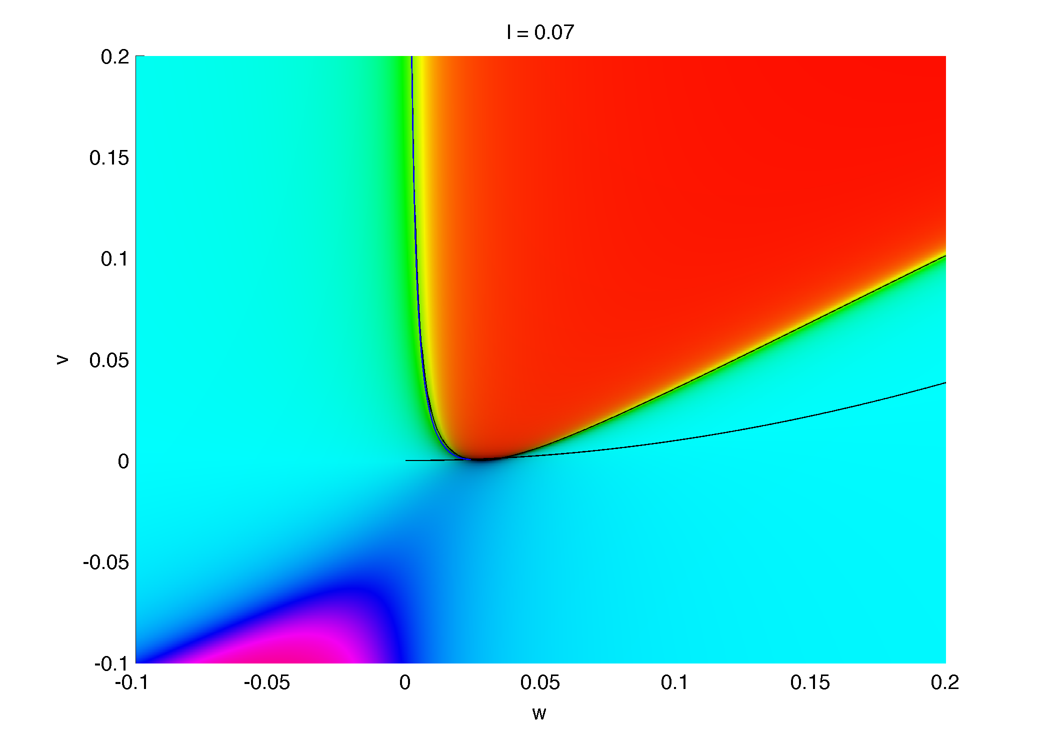
p = 90 400 3 5

Phase portrait (vector field is plotted in HSV, isoclines in black and trajectory in white), the hopf bifurcation occurs when the two isoclines meet at the inflexion point of the w one :

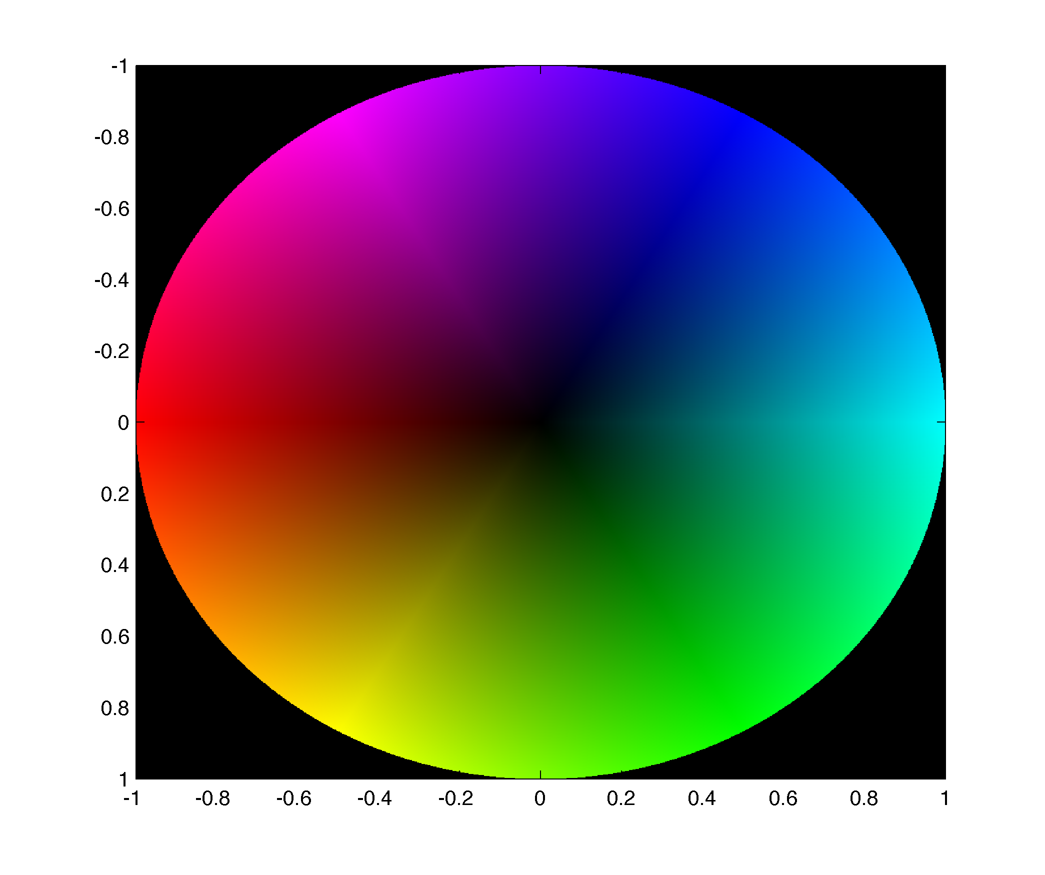
Colormap :

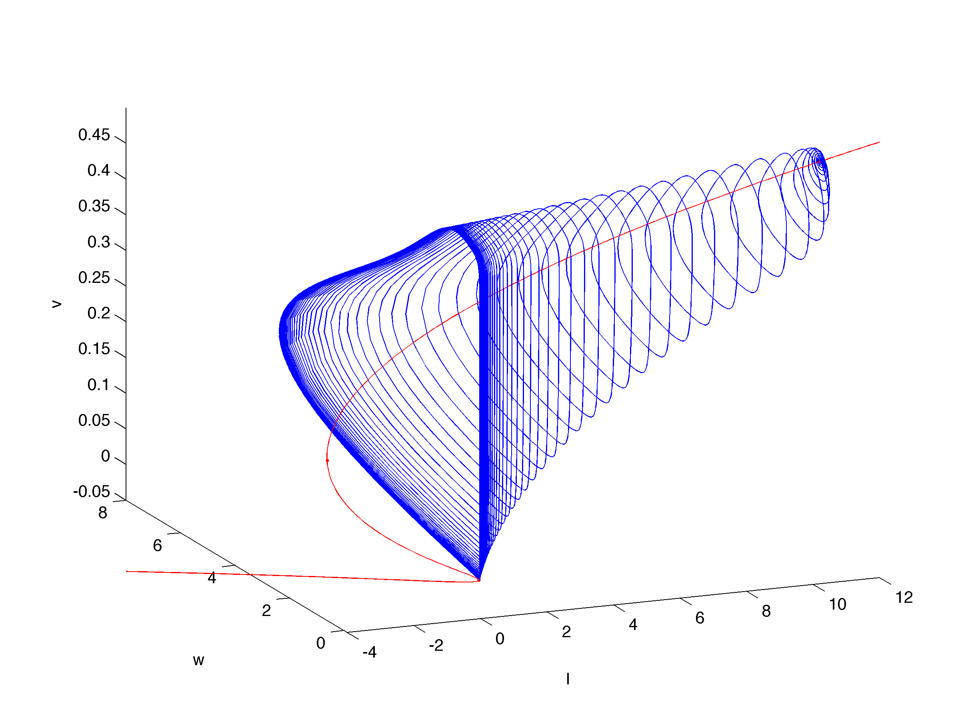
Bifurcation diagram :

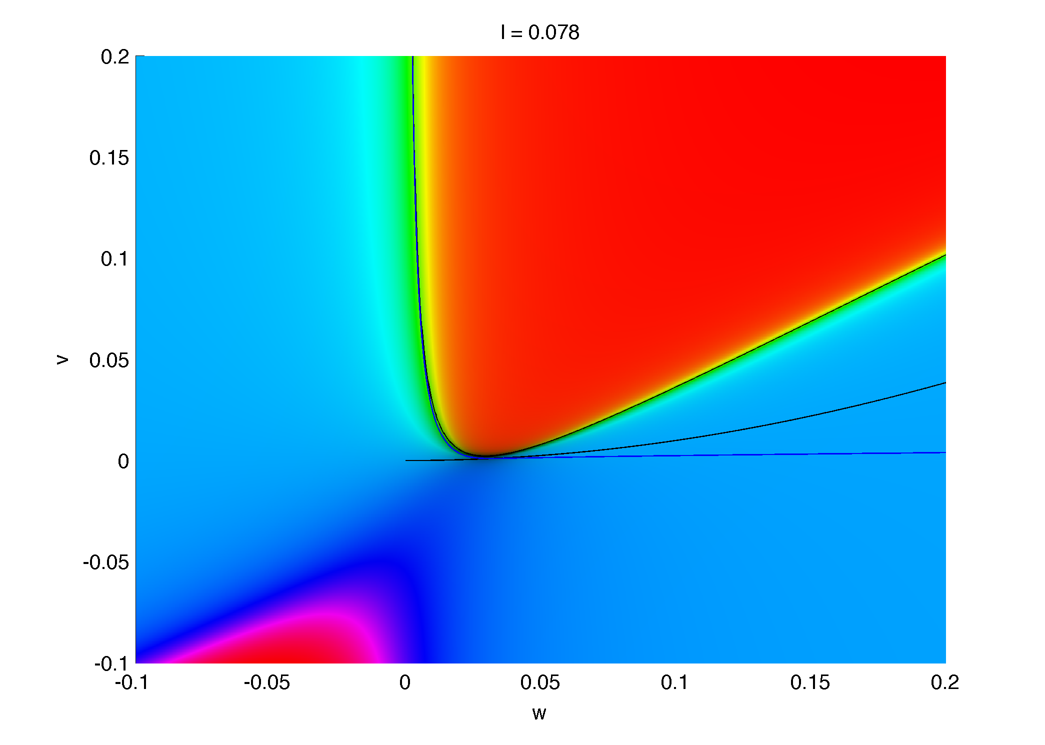
The limit cycle seems to disappear trough a sniper bifurcation near I = 0.073 (trajectory in blue) :

 The stable fixed point then move to (0,0) as I goes to zero.