The model :

$latex \displaystyle{ \Large \dot{w} = W}$

$latex \displaystyle{ \Large \dot{v} = V}$

$latex \displaystyle{ \Large \dot{A} = B }$

$latex \displaystyle{ \Large \dot{W} = 1/\epsilon ( - \alpha_w \frac{w^2}{1 + w^2} + \gamma_{vw} ~ v \frac{w}{k + w} + \lambda_w ~w - A - c W )}$

$latex \displaystyle{ \Large \dot{V} = 1/\epsilon( -\frac{w^2}{1 + w^2} + v - c V )}$

$latex \displaystyle{ \Large \dot{B} = 1/ D ( -\alpha_A w + \lambda_A ~A - c~B )}$

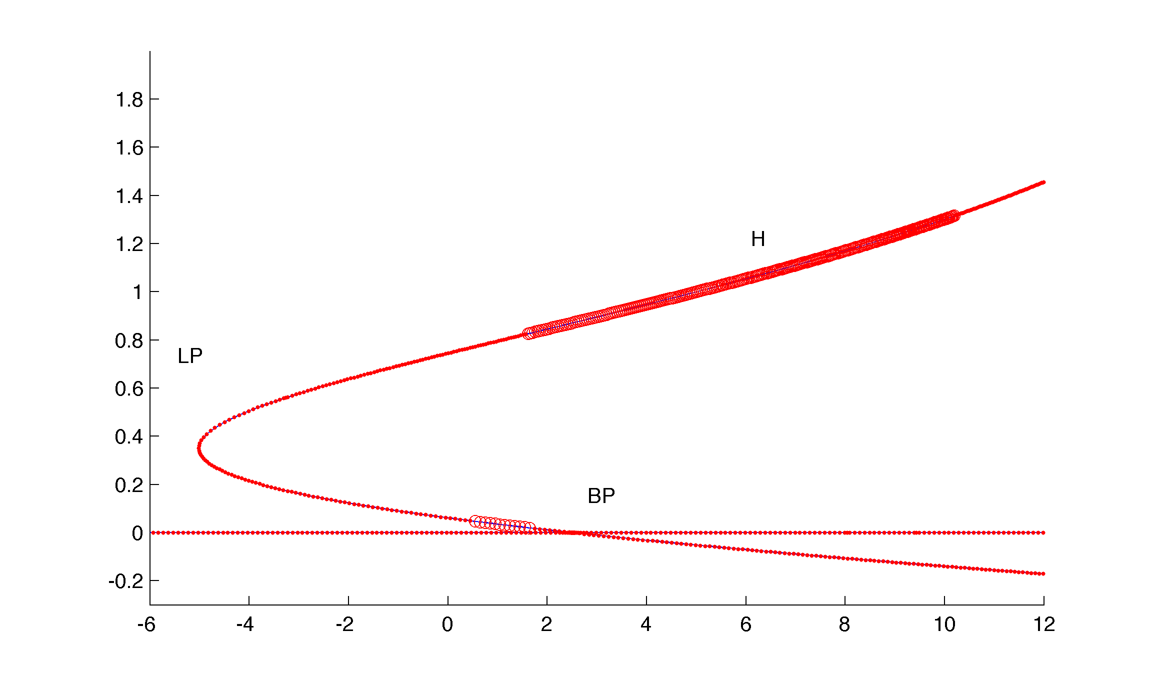
The bifurcation diagram is the same than the 3D one (except the stability). On the main curve 3 eigenvalues are always negative, one always positive and the 2 other change stability at the H,LP and BP bifurcation.

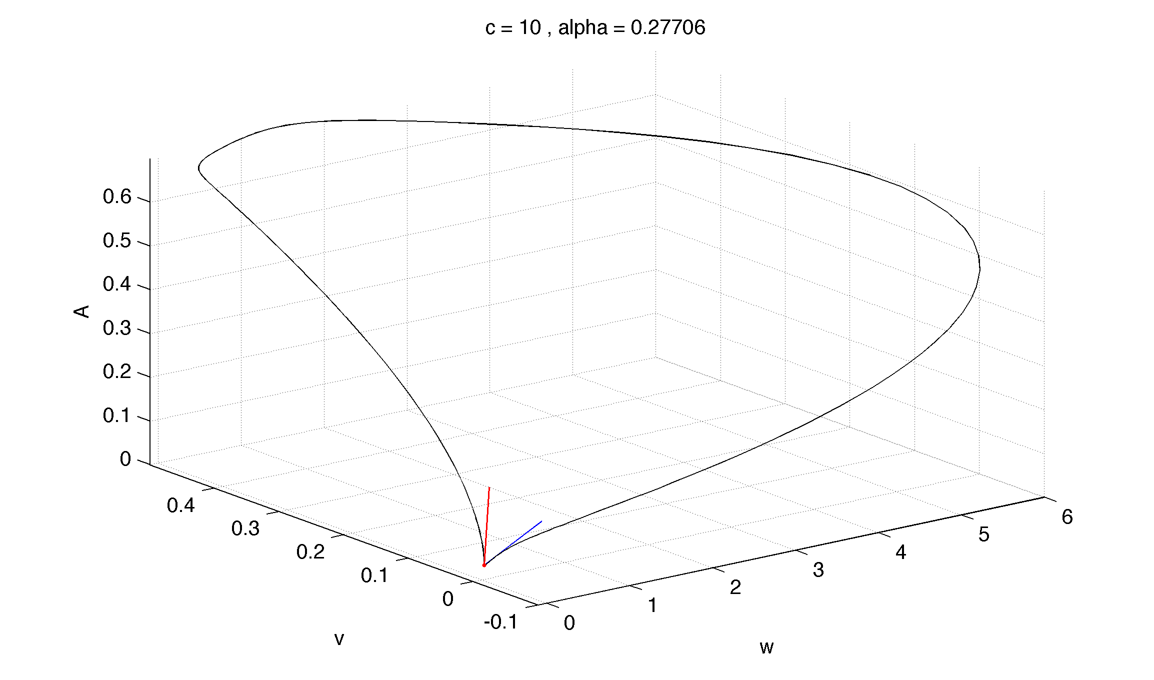
At c=10 the homoclinic orbit connects to the non zero fixed point. All eigenvalues are real. This fixed point has a 2 dimensional stable manifold and a 4 dimensional unstable one (here the projections of two eigenvectors are shown) :

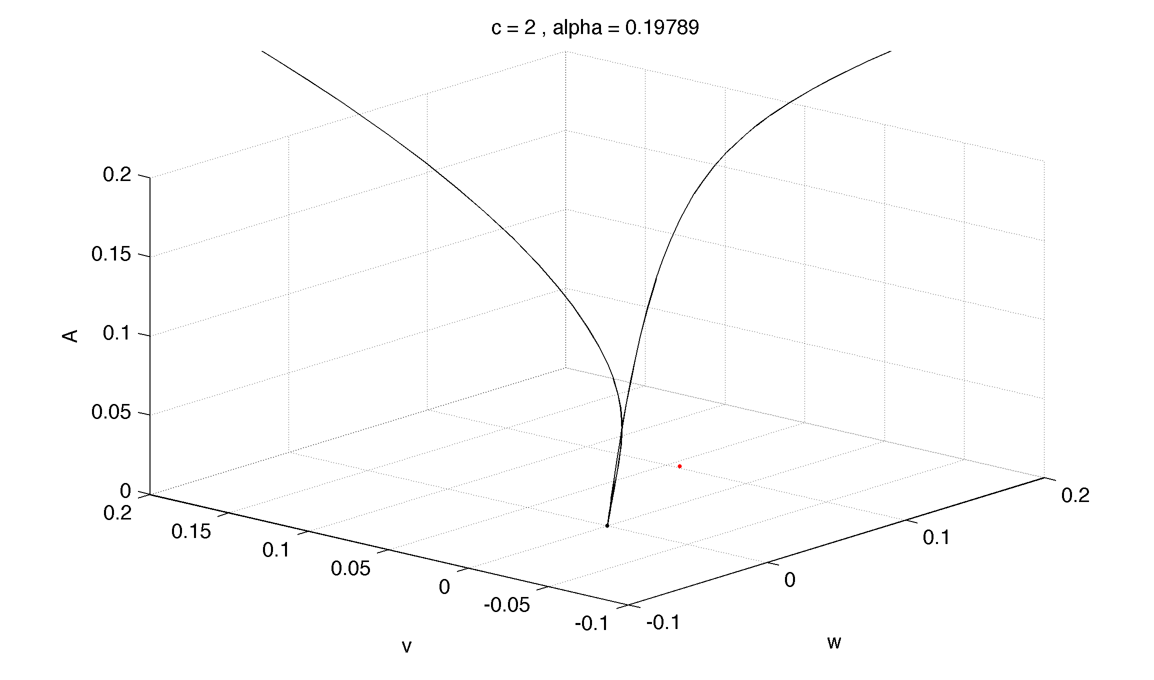
Near c=2.7 the homoclinic orbit start to pass close to the zero fixed point and seems to touch both fixed point at c=2.52 :

Then bellow homoclinic connect to the zero fixed point only :

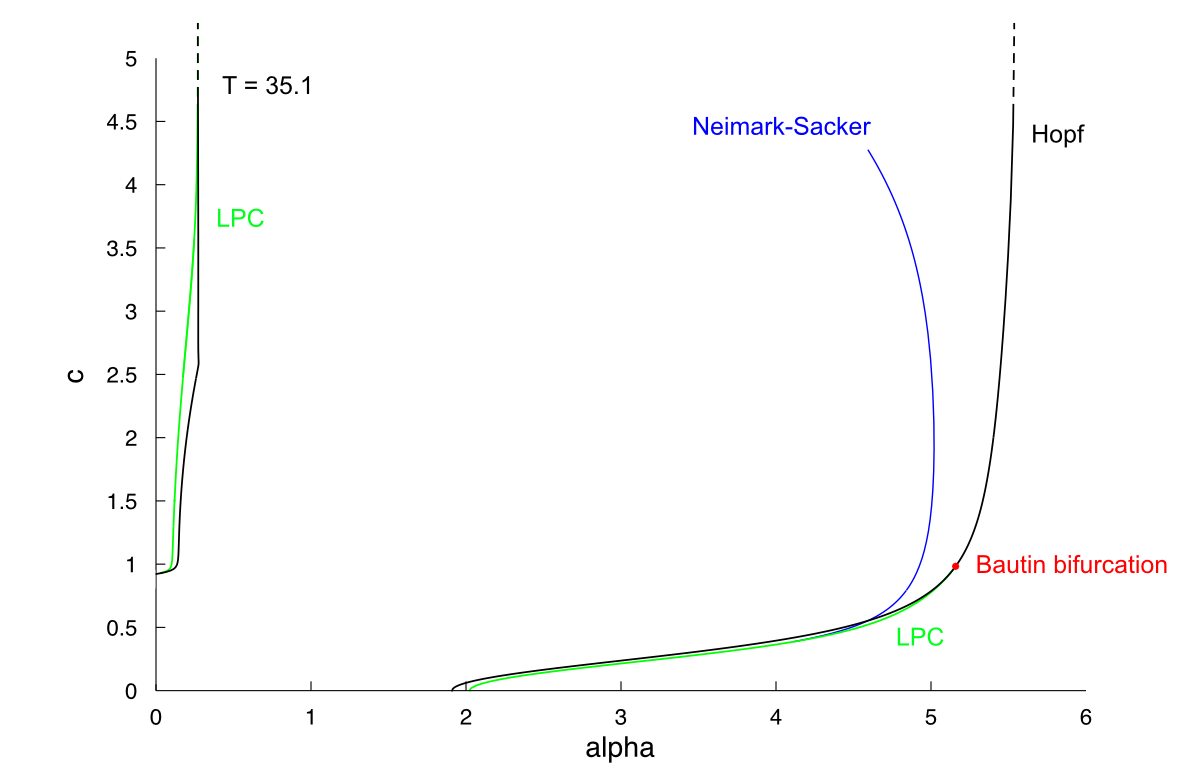
Thus there exists two different homoclinic branches that meet near c=2.5 and form an heteroclinic loop. A similar scenario was found in this paper.