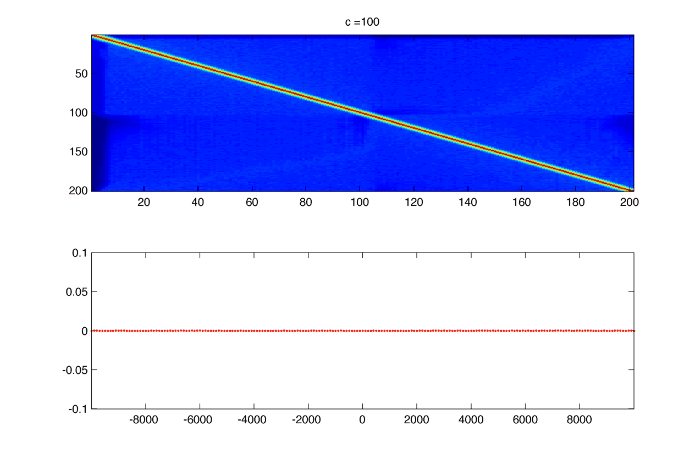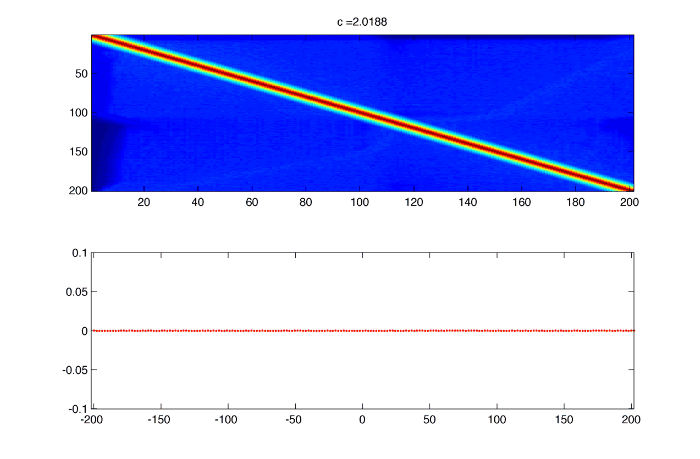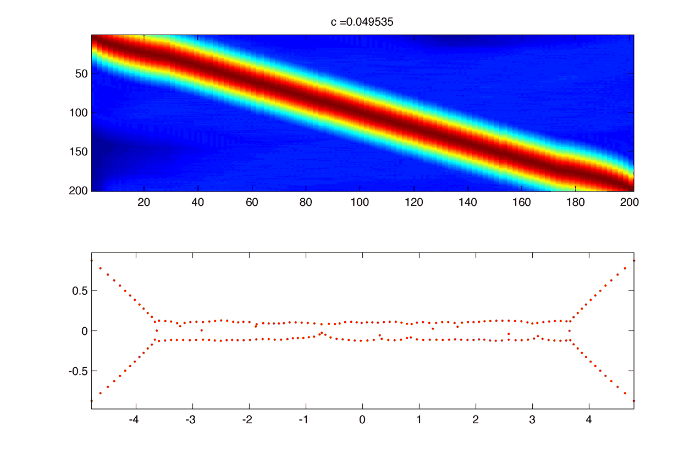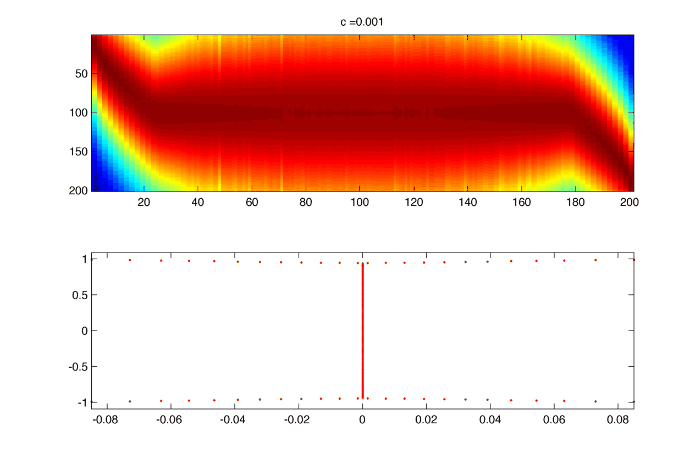
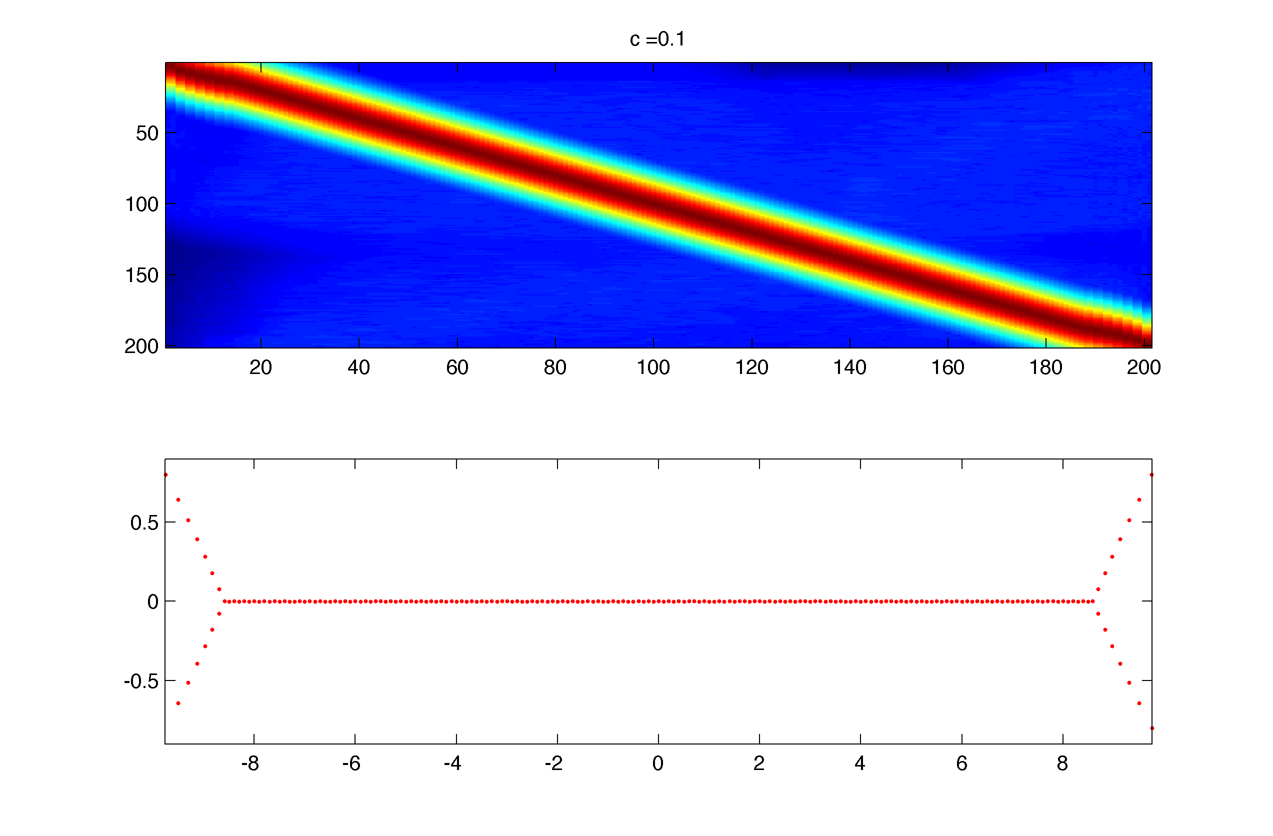
Simple case

We want to find the spectrum of the differential operator :

 $latex \displaystyle{ \Large L = c~\partial_{x} + cos(x)  - \lambda}$

The eigenvalue problem is :

 $latex \displaystyle{ \Large L f = 0}$

This give the ODE :

 $latex \displaystyle{ \Large  f_x = -\frac{1}{c}( cos(x)~f - \lambda f)  }$

The solutions are :

 $latex \displaystyle{ \Large  f(x) = c_1 e^{ \lambda / c ~ x} e^{ -sin(x) / c }  }$

As c goes to zero  $latex \displaystyle{ \Large  e^{ -sin(x) / c } }$ gets really peaked, and the spectrum really wide so that it cannot be

represented in the truncated representation :

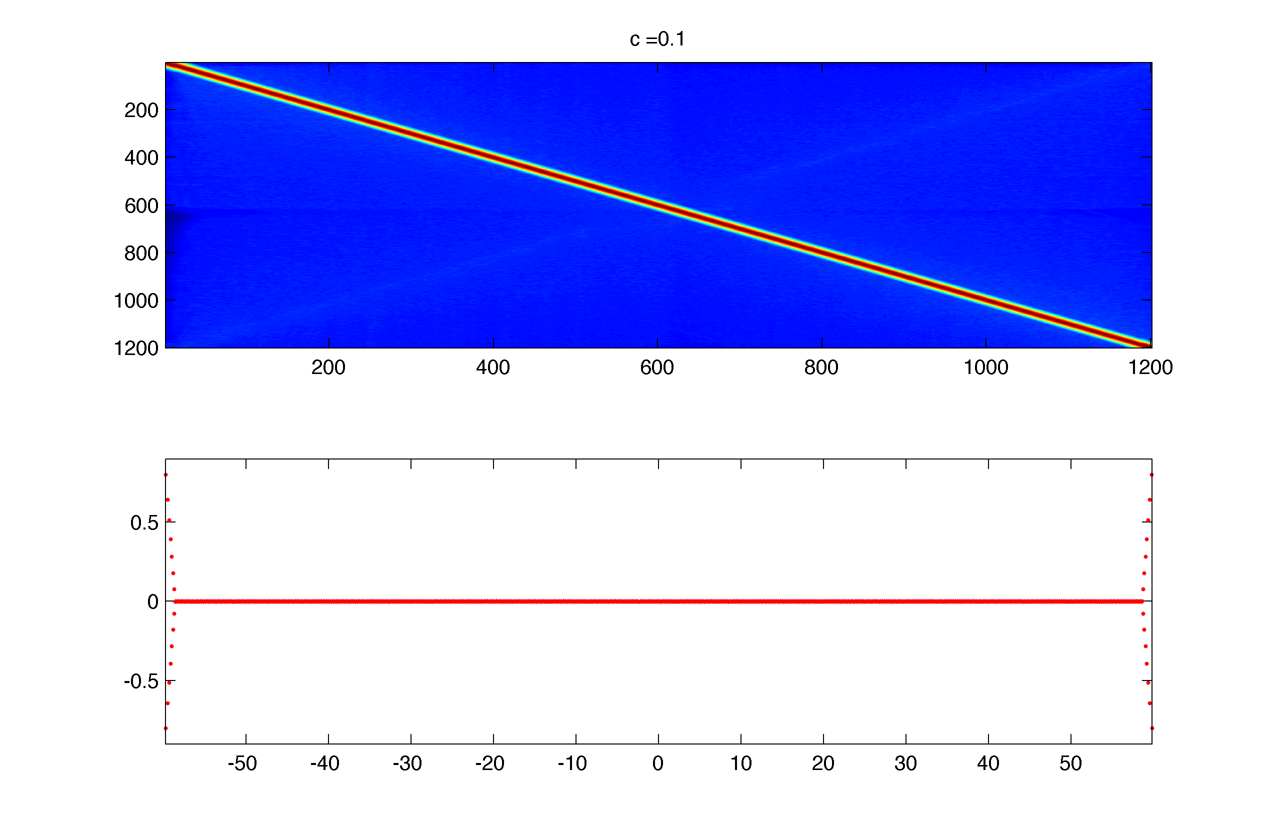
However increasing the number of frequencies doesn't really solve the problem :

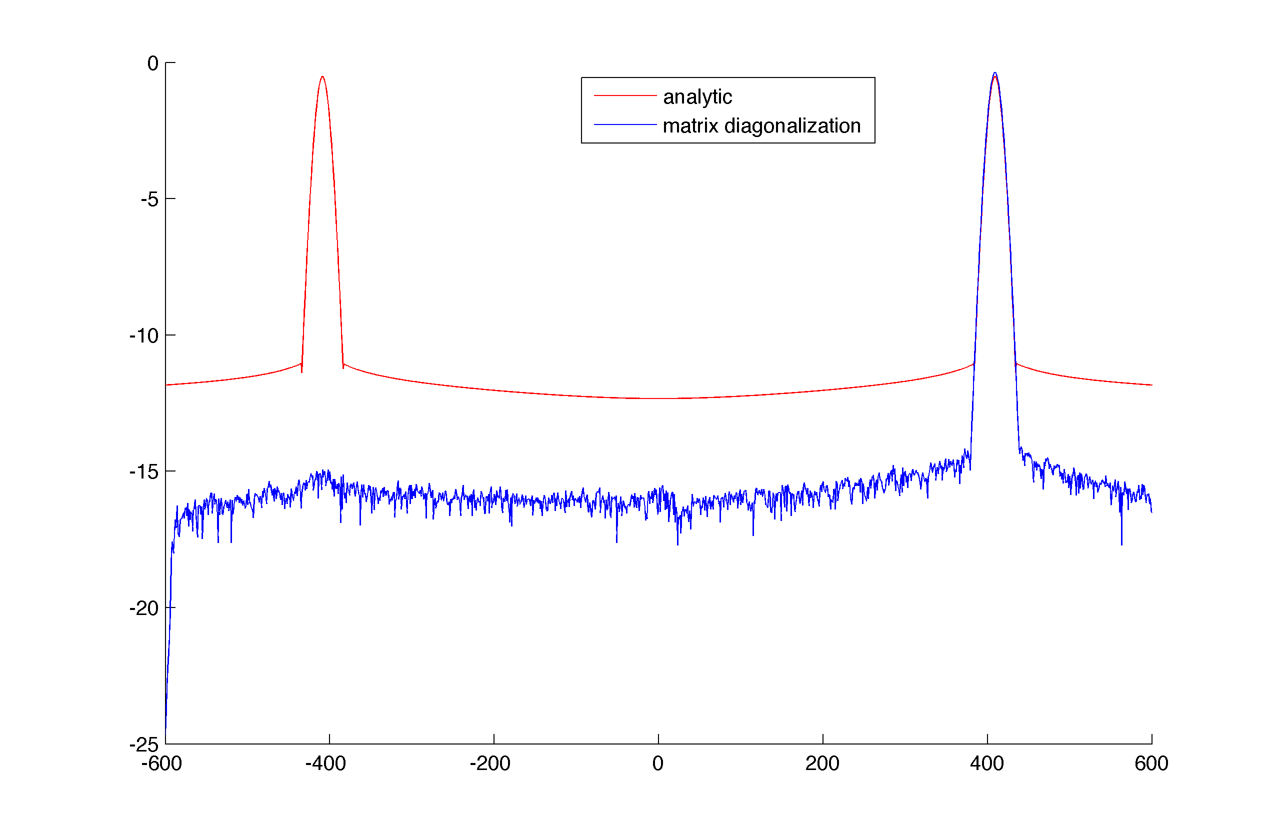
The spectrum and the eigenfunctions seems to match the ones computed from matrix diagonalization, expect for  some hermitian symmetry :