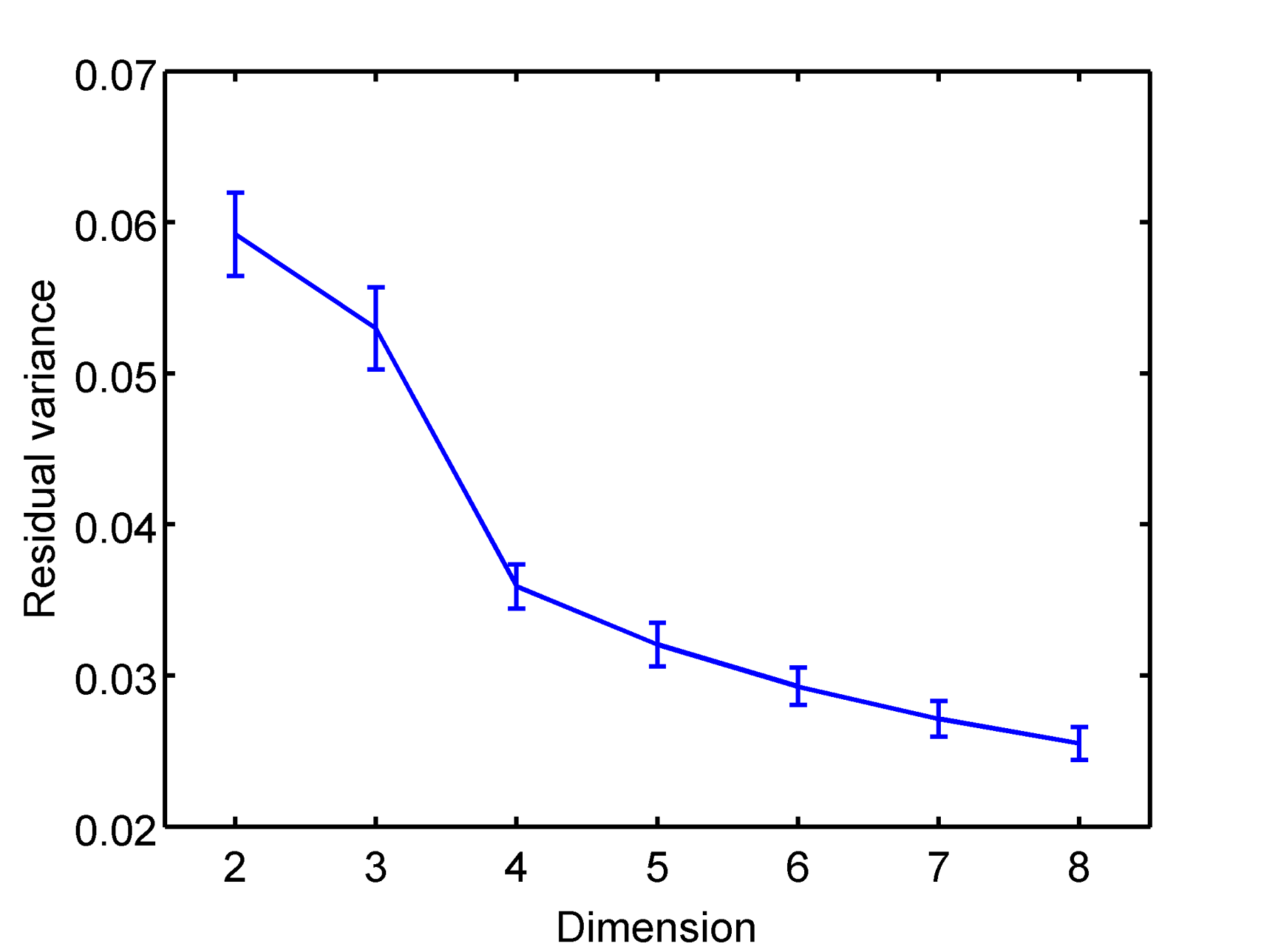
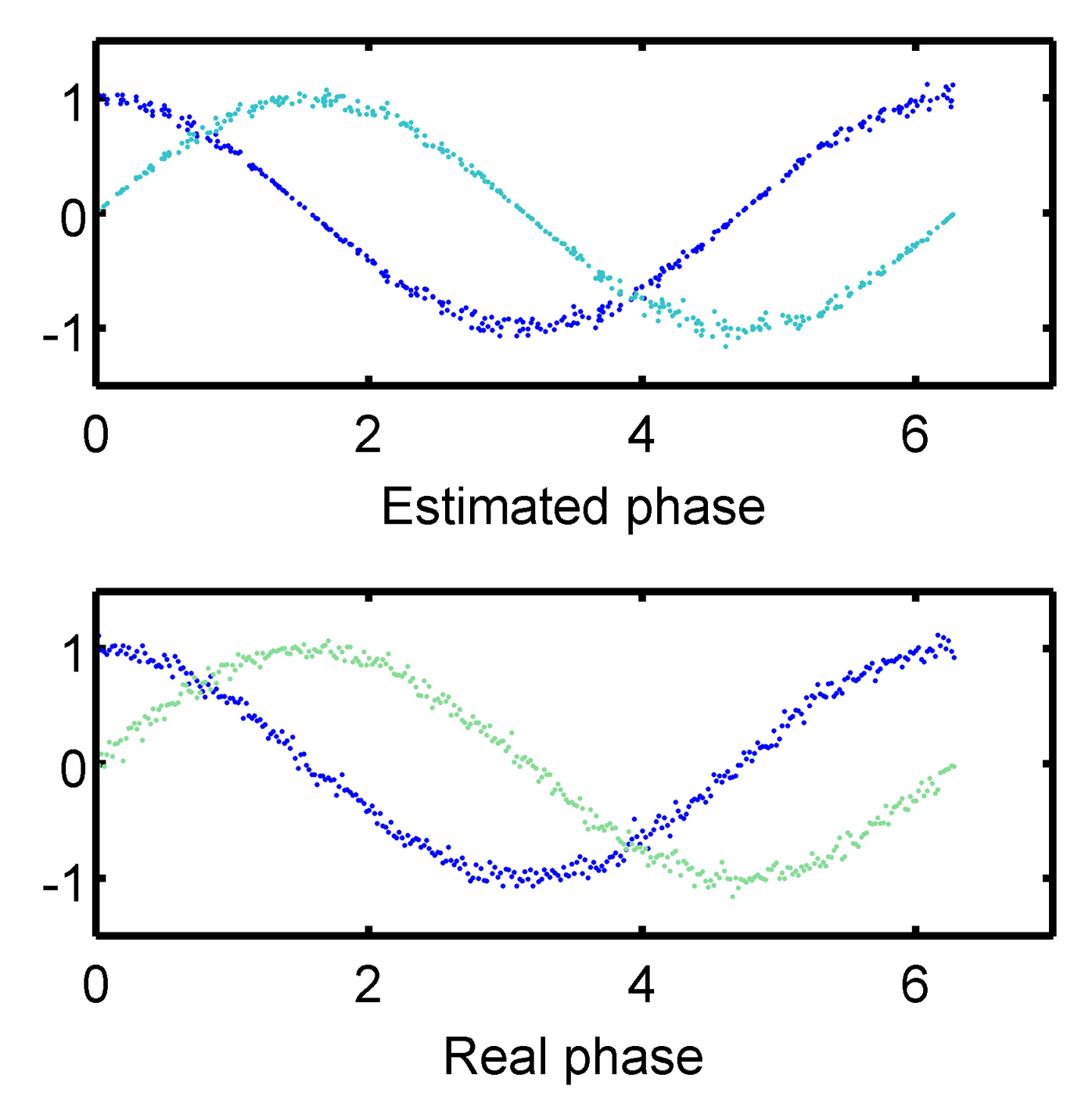
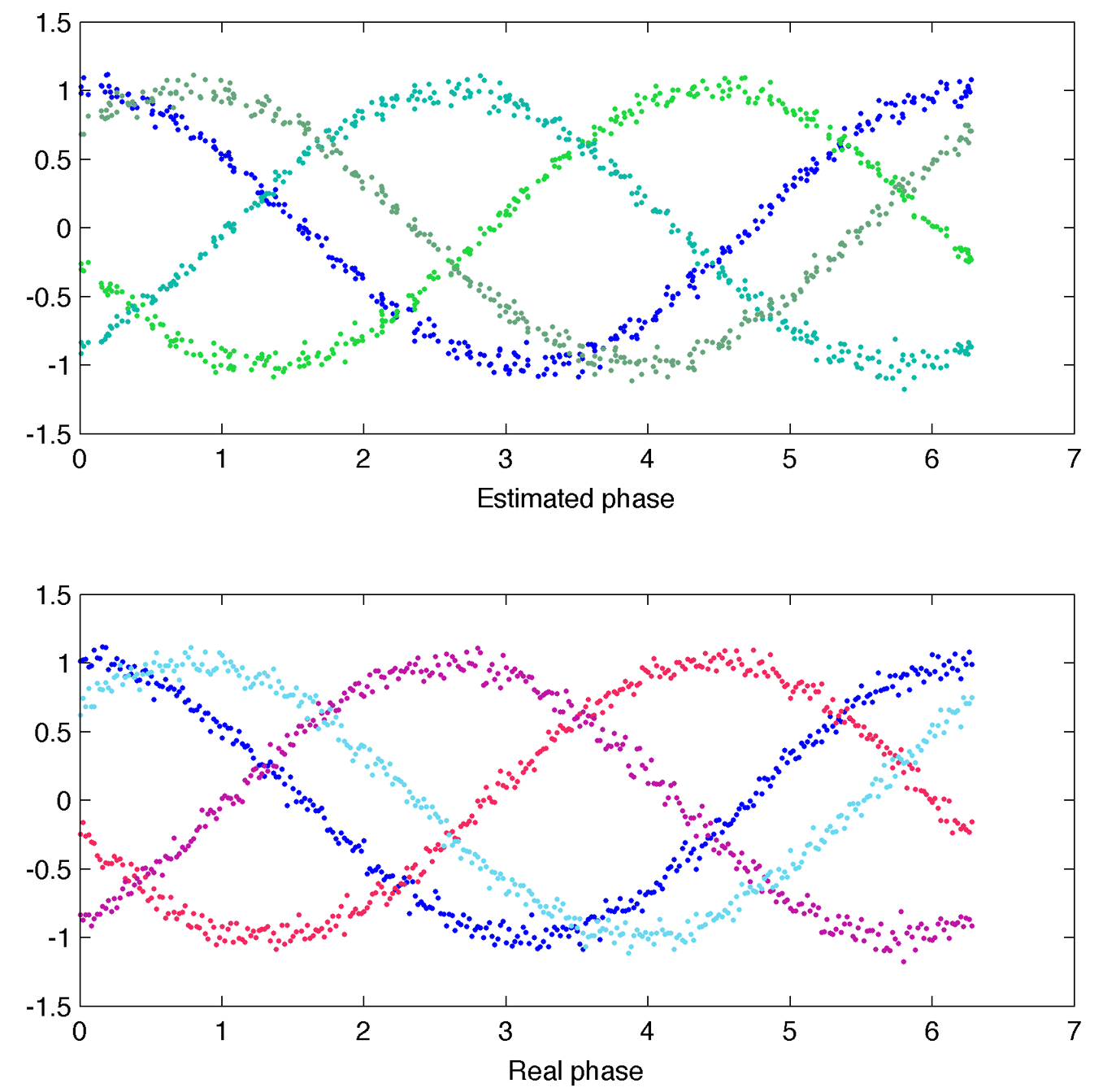
Phase recovery from static data : toy model

We generate data x :

 $latex \displaystyle{\vec{x_i} = \vec{r} \cos( \theta_i + \vec{\phi}) + \vec{\xi_i}}$ where x, r and phi are N dimensional vectors, i denoting measurement index and xi is a normally distributed centered random variable with covariance matrix B (possibly depending on theta).

Then data x are randomly mixed so that any information about the phase is lost. The question is : can we recover information about the phase and the covariance matrix B looking only at measurement x, and if so, how does it depend on dimension N.

In one dimension it is not possible since the function acos is multivalued.

To solve this problem in higher dimension we fit the model :

$latex \displaystyle{\vec{x_i} = \hat{r} \cos( \hat{ \theta_i } + \hat{\phi}) }$ to the data using least square euclidian distance. The estimated phase can the be compared to the true one, and residual variance can be computed for different dimension :

2D :

4D :