FitzHugh Nagumo

$latex \displaystyle{ \Large v_t = v(v-1)(\alpha -v) - w + I + D v_{xx} }$

$latex \displaystyle{ \Large w_t = \epsilon(v-\gamma w) }$ 

Following Champneys 2007, $latex \displaystyle{ \Large (D, \alpha, \epsilon, \gamma) = (5, 0.1,0.01,1) }$

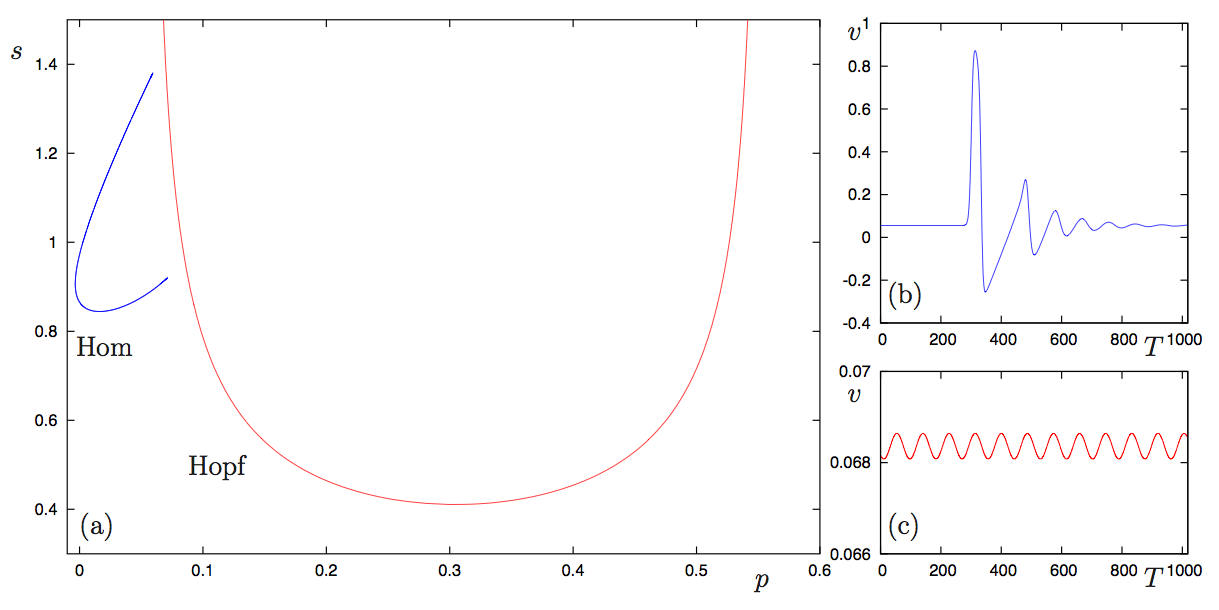
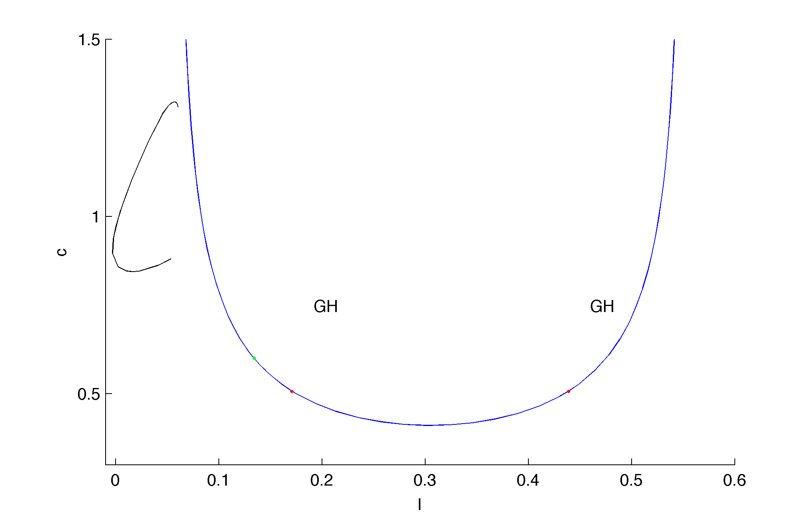
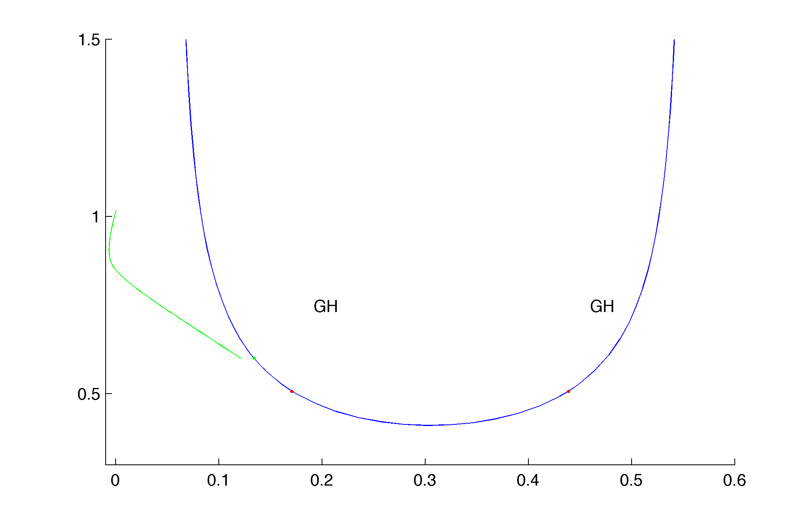
The U curve, GH are bautin bifurcation indicating the existence of LPC, the black line is a limit cycle with large period, close to the homoclinic orbits :

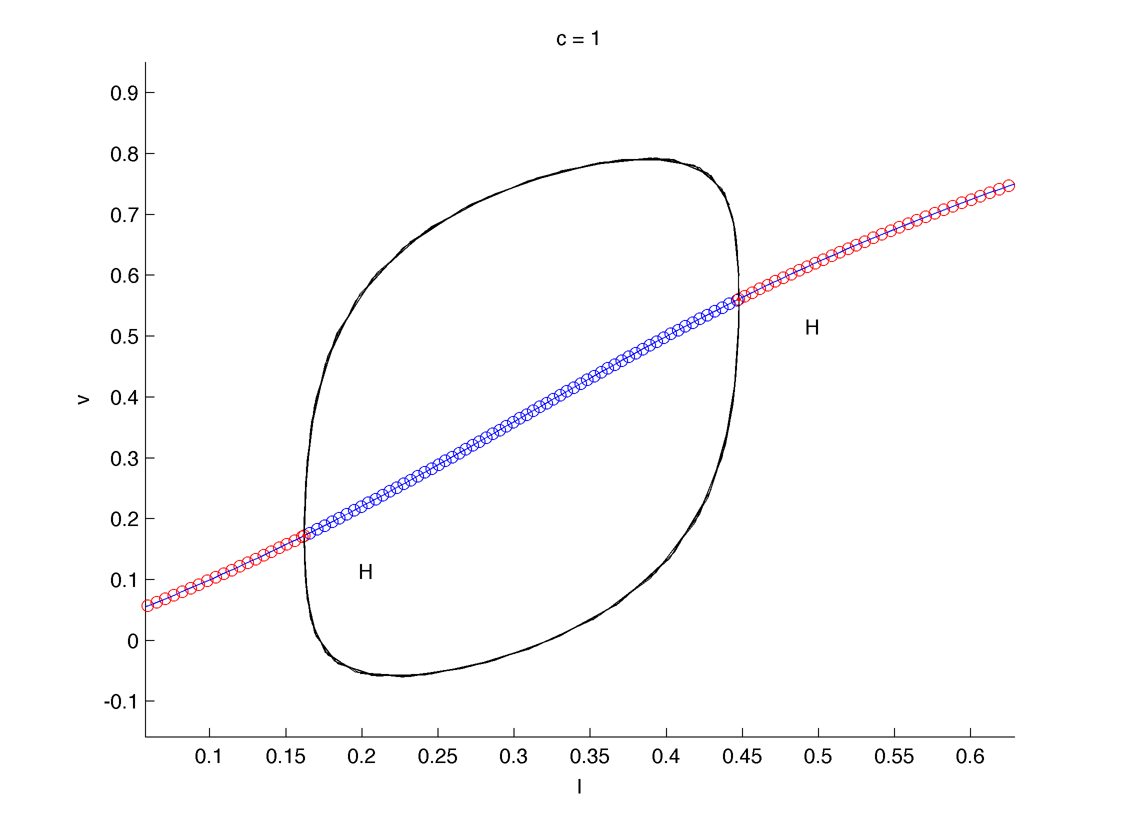
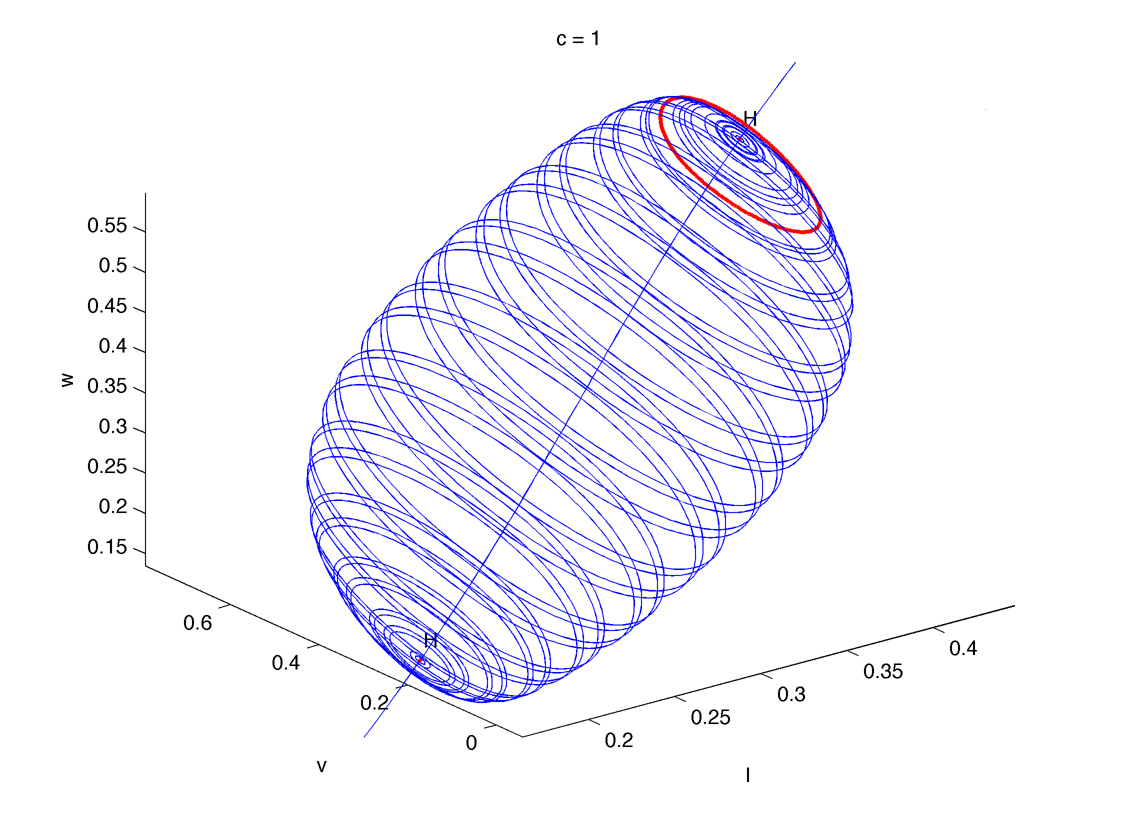
For low speed the limit cycle joins the two Hopf bifurcation  (color indicate the period, the two first plots are a bit "artistic") :

When c increase LPCs appear (as we pass the Bautin bifurcation the first Hopf bifurcation change from supercritical to subcritical) :

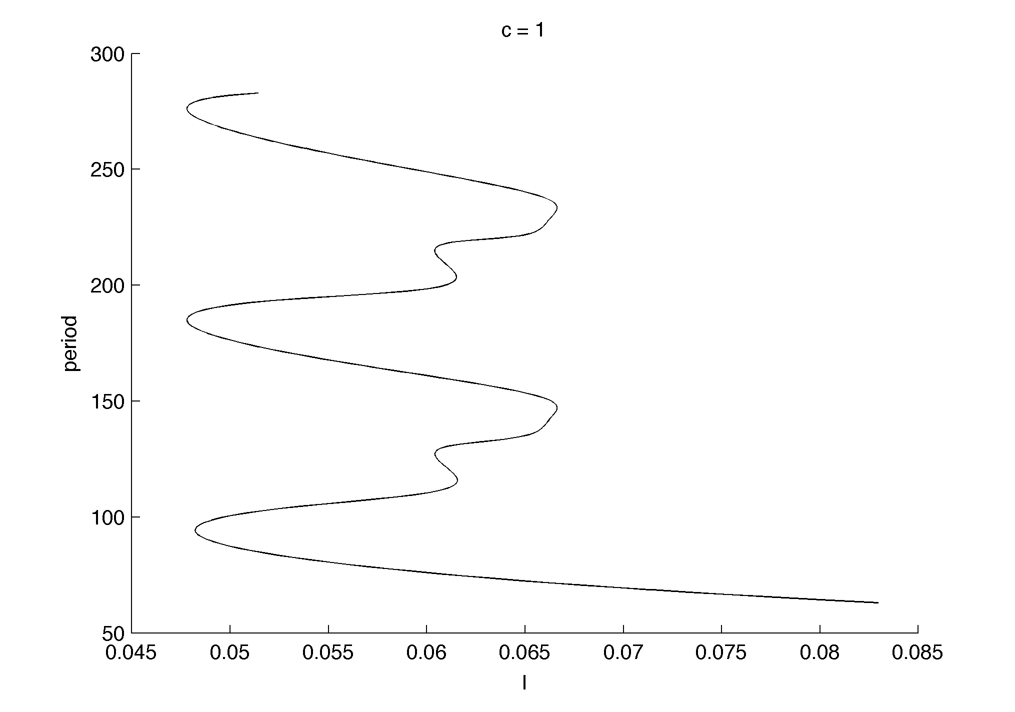
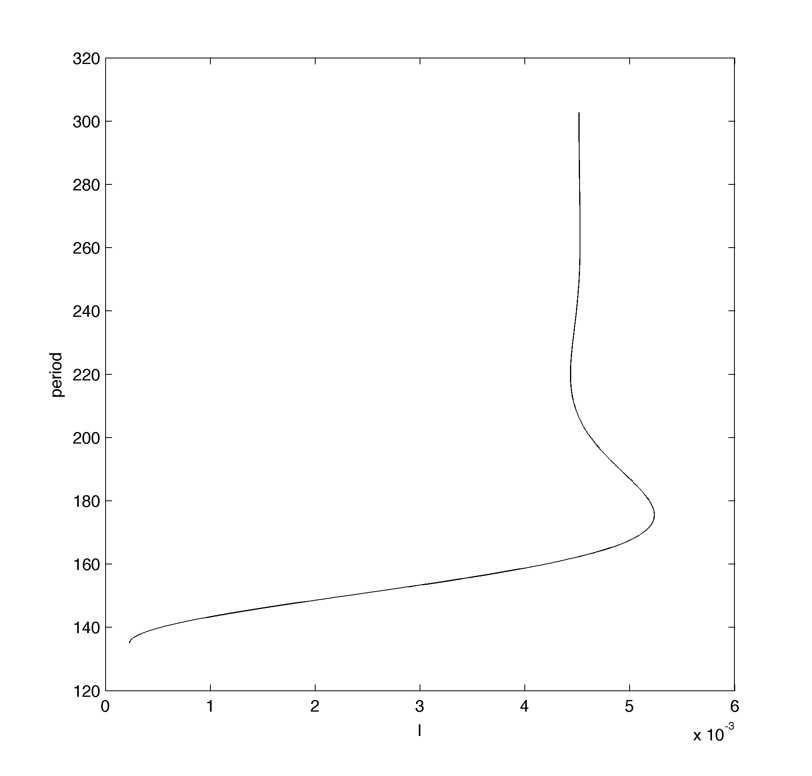
The period increase near the LPC and the trajectories become more spiky :

At some point the continuation is unable to join the two Hopf bifurcations, the period goes to infinity (through periodic LPCs) :

The same plot from Champneys. "The form of this curve indicates that the periodic orbit approaches a set of homoclinic tangencies to a limit cycle (see e.g. [20])"

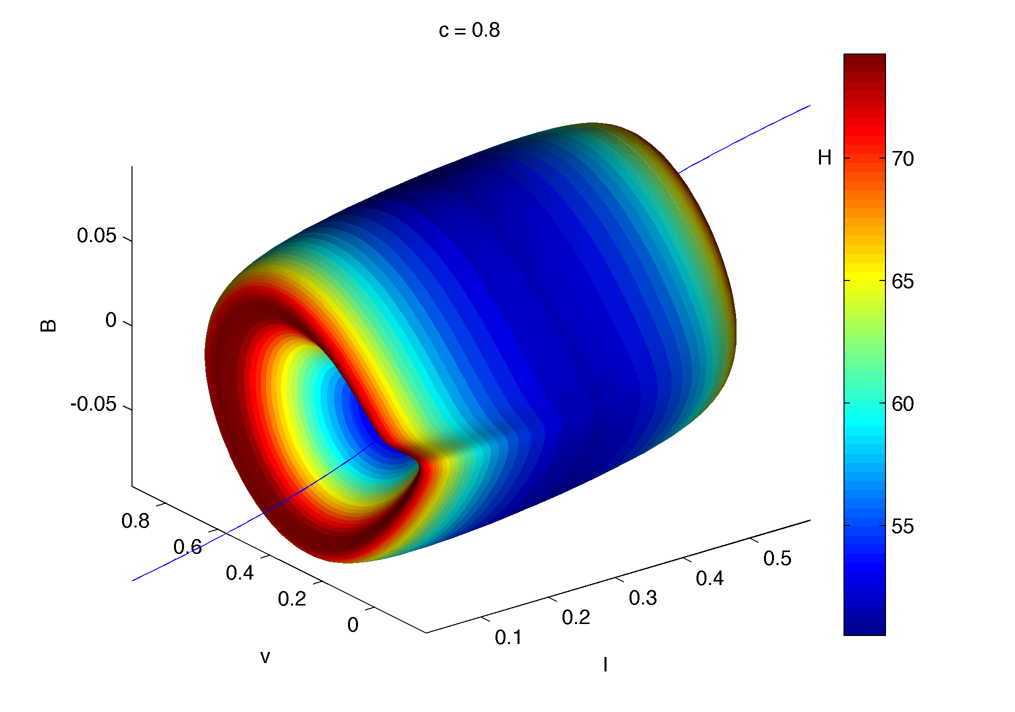
The limit cycle also does a little loops (nice movie, nice movie 2) :

We can find the homoclinic to saddle orbits by continuing one of the LPC curve :

And then continuing one of the limit cycle :

Following the limit cycle with large period (~300) gives a good idea of the homoclinic orbit :

$latex \displaystyle{ \Large  v_t =  v(v-1)(\alpha -v) - w + I + v_{xx} }$  

$latex \displaystyle{ \Large  w_t = \epsilon(v-\gamma w) }$

with $latex \displaystyle{ \Large  (\alpha, \epsilon, \gamma) = (0.1,0.1,1) }$

***

$latex \displaystyle{ \Large  z = x - ct  }$ :

$latex \displaystyle{ \Large  v_z =  B }$  

$latex \displaystyle{ \Large  B_z =  -v(v-1)(\alpha -v) + w - I -c B }$   

$latex \displaystyle{ \Large  w_z = \frac{-1}{c} \epsilon(v-\gamma w) }$

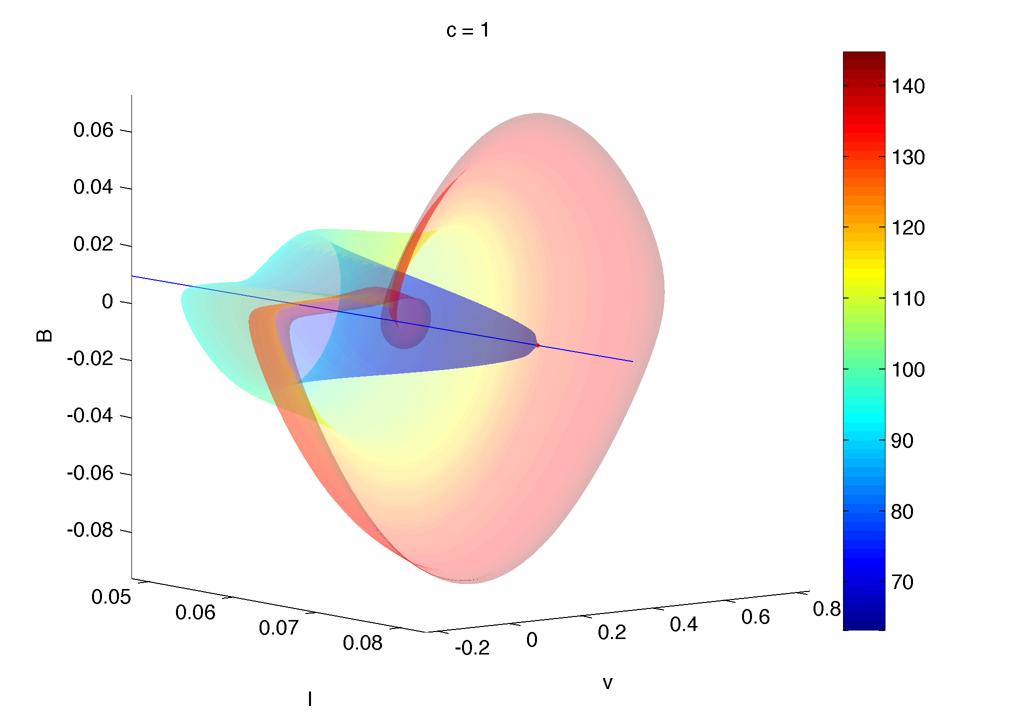
Continuation in I : 

(the red circle is just the end of the continuation, but there is LPC near the hopf points)

***

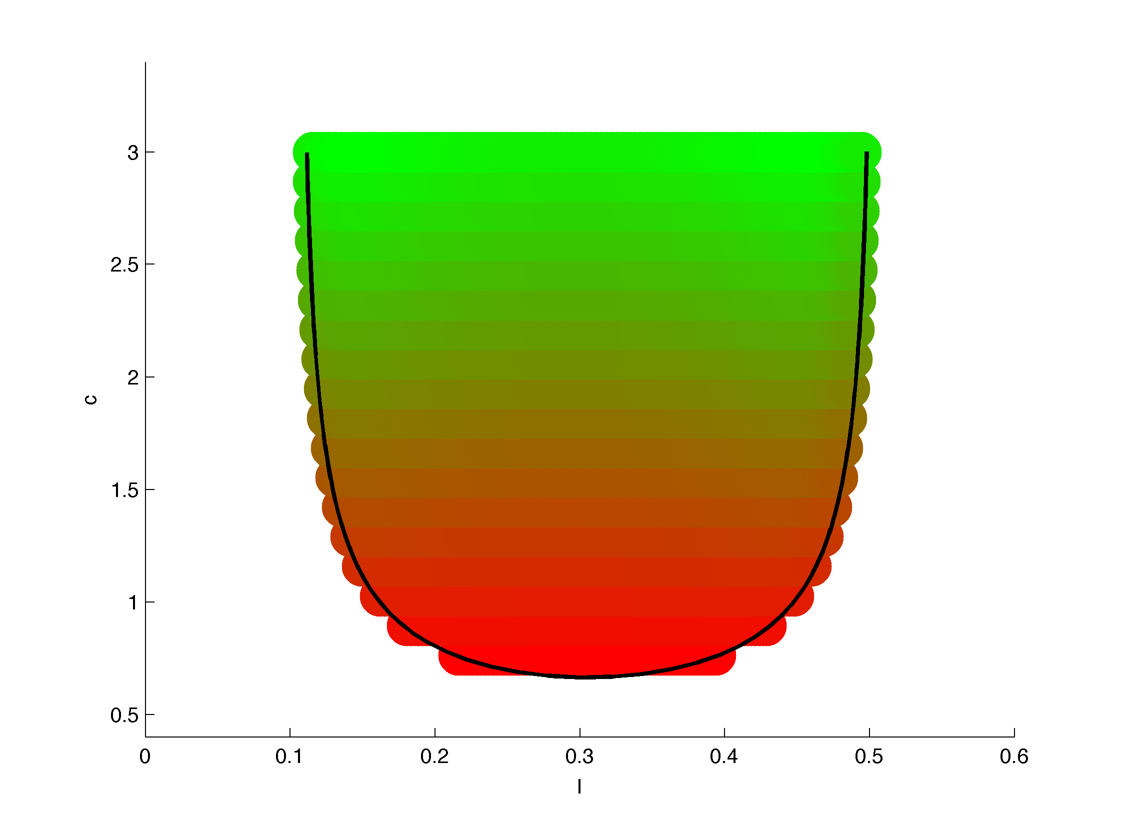
U curve of hopf point with period (red lower, green higher) :