Parameters 

In chambers of 100x100 $latex \displaystyle{\mu m ^2}$ the medium is synchronized.

Temporal period : 52–90 min

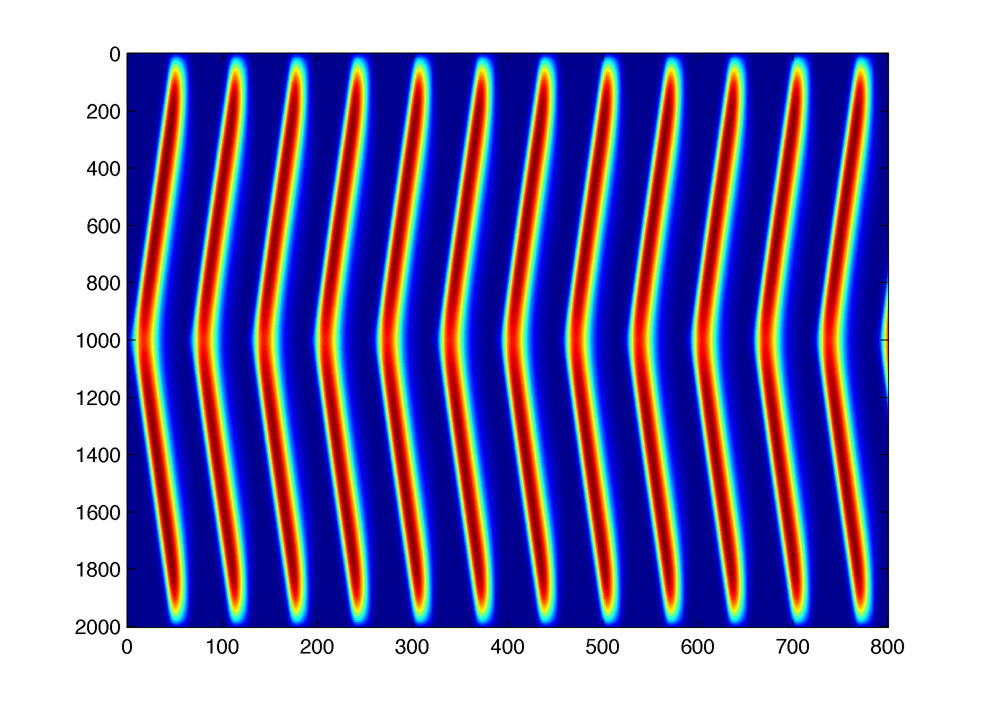
Big chambers with waves are 2000 $latex \displaystyle{\mu m}$ long.

Waves speed is ~ 5-30 $latex \displaystyle{\mu m }$ per min.

Diffusion constant : 2'000-10'000 $latex \displaystyle{\mu m ^2 }$ per min. 

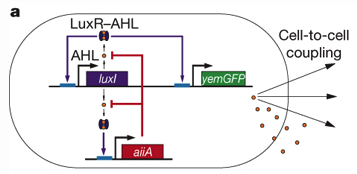
Detailed model :

$latex  \displaystyle \frac{d}{dt}AHL_{in}=k_{1}LuxI+k_{in}AHL_{out}-(k_{out}+\lambda_{1}+k_{2})AHL_{in}-\gamma AiiA\frac{AHL_{in}}{t_1+AHL_{in}} $  (1)

$latex  \displaystyle \frac{d}{dt}AHL_{out}=-(k_{in}+\lambda_{2})AHL_{out}+k_{out}AHL_{in}+\frac{d^{2}}{dx^{2}}DAHL_{out}$ (2)

$latex  \displaystyle \frac{d}{dt}LuxR:AHL=k_{2}AHL_{in}-\lambda_{3}LuxR:AHL$ (3)

$latex  \displaystyle \frac{d}{dt}LuxI=\alpha_{1}LuxR:AHL^{2}/(t_{2}^{2}+LuxR:AHL^{2})-\lambda_{4}LuxI$ (4)

$latex  \displaystyle \frac{d}{dt}AiiA=\alpha_{2}LuxR:AHL^{2}/(t_{2}^{2}+LuxR:AHL^{2})-\lambda_{5}AiiA $ (5)

Simplifications :

Neglected AHL:LuxR complex formation : AHL_in directly activates LuxI and AiiA (Remove Eq. 3)

Neglected LuxI, AHL:LuxR, so AHL_in directly activates itself (Remove Eq. 4)

Simplified model :

$latex \displaystyle \frac{d}{dt}AHL_{in}=\alpha_{1}AHL_{in}^{2}/(t_{2}^{2}+AHL_{in}^{2})+k_{in}AHL_{out}-(k_{out}+\lambda_{1}+k_{2})AHL_{in}-\gamma AiiA\frac{AHL_{in}}{t_1+AHL_{in}}$

$latex \displaystyle \frac{d}{dt}AiiA=\alpha_{2}AHL_{in}^{2}/(t_{2}^{2}+AHL_{in}^{2})-\lambda_{5}AiiA$

$latex \displaystyle \frac{d}{dt}AHL_{out}= k_{out}AHL_{in} -(k_{in}+\lambda_{2})AHL_{out} +\frac{d^{2}}{dx^{2}}DAHL_{out}$ 

Renaming variables and parameters :

$latex \displaystyle \frac{d}{dt}w=\alpha_{1}w^{2}/(t_{2}^{2}+w^{2})-(\lambda_{1}+k_{out})w-\gamma v\frac{w}{t_1+w}+k_{in}A $  

$latex \displaystyle \frac{d}{dt}v= \alpha_{2}w^{2}/(t_{2}^{2}+w^{2})-\lambda_{2}v $  

$latex \displaystyle \frac{d}{dt}A=k_{out}w-(\lambda_{3}+k_{in})A+D\frac{d^{2}}{dx^{2}}A$ 

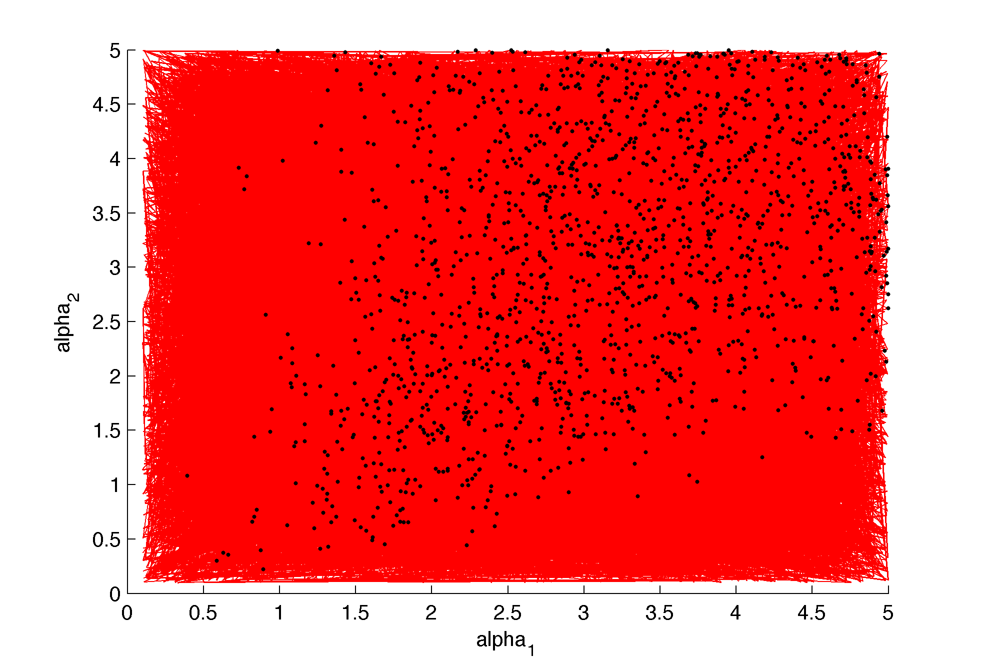
$latex \lambda_{1}$ is the export, degradation and complex formation of internal AHL

$latex\lambda_{3}$  is the import and degradation of external AHL

$latex k_{in}$ is the import rate of external AHL 

In order to find good parameters I sampled randomly a subset of the parameters space (red) and looked for good oscillations (black).

More discussion in this pdf.

The parameters that correlate the more are $latex \displaystyle \alpha_1$ with $latex \displaystyle \alpha_2$ and $latex \displaystyle \alpha_1$ with $latex \displaystyle \gamma $ :

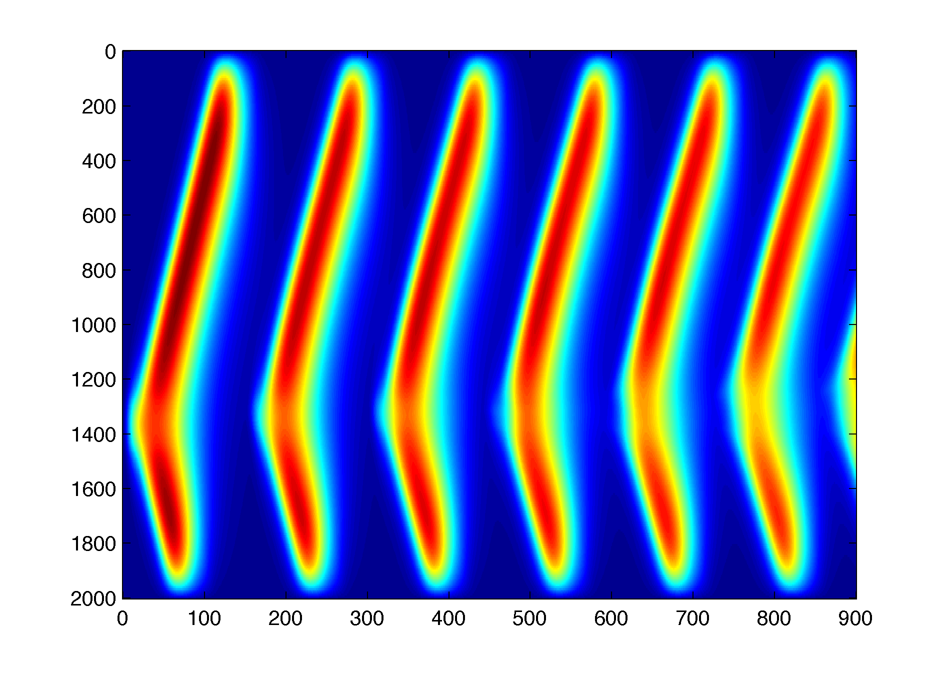
Some simulations :

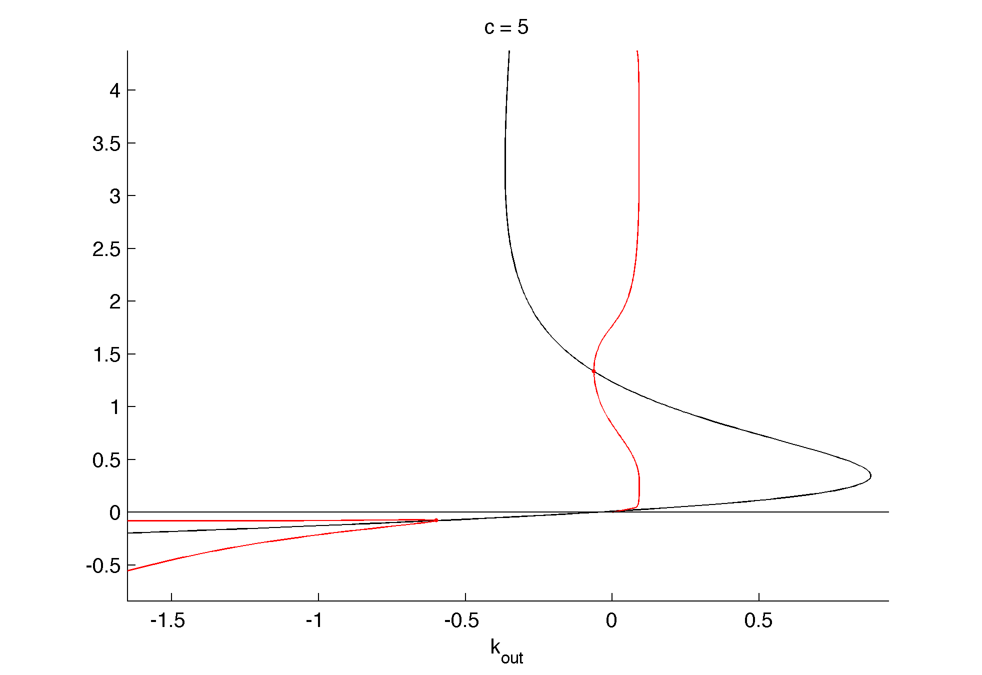
Bifurcation in k_out (production of external AHL) :

Simulation : Using parameters like $latex \lambda_{1}= 1/30 ~ [min^{-1}]$  :

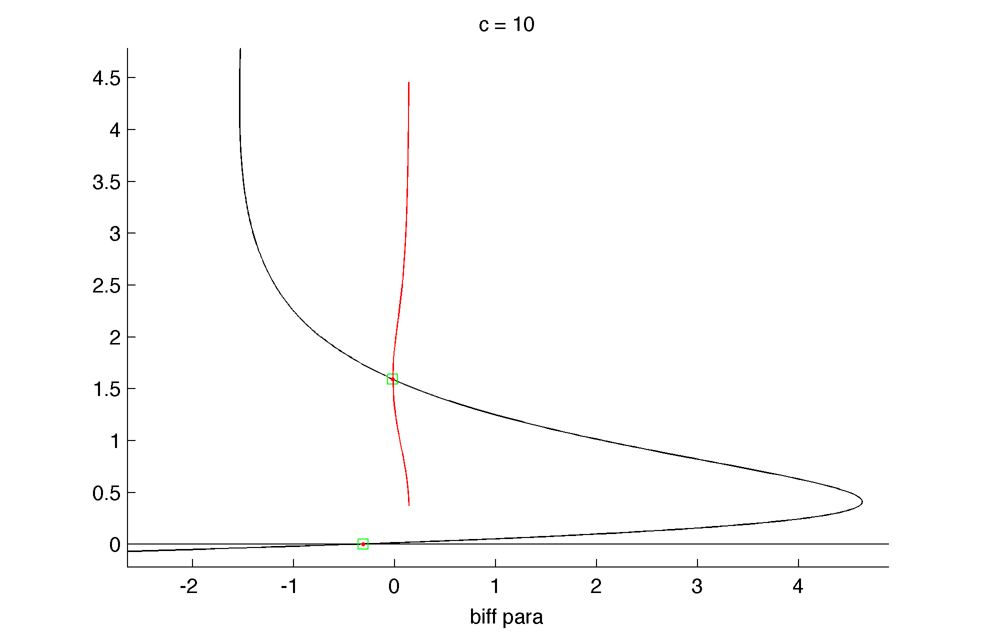
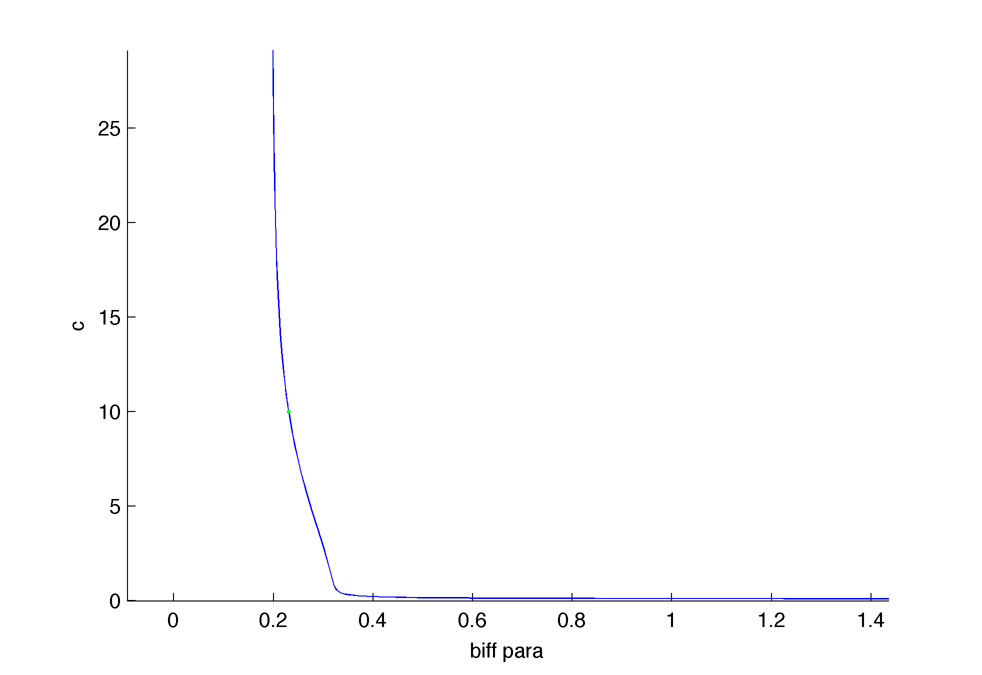
Bifurcation diagram in $latex \displaystyle \lambda_{3} $ :

Parameters (in the same order than in the equation) :   10.0000 0.5000 0.0286 0.0286 0.2000 1.0000 0.0286 12 0.5000 0.0400 0.0286 0.0250 1.5000(*1000)

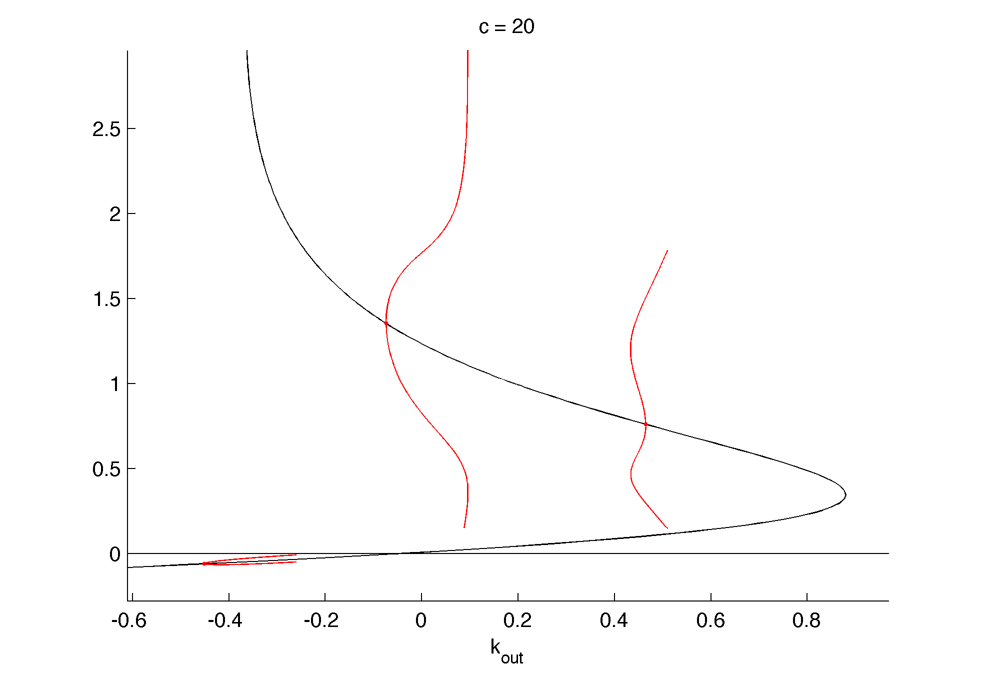
 Hopf-bifurcations in the (k_out, c) plane :

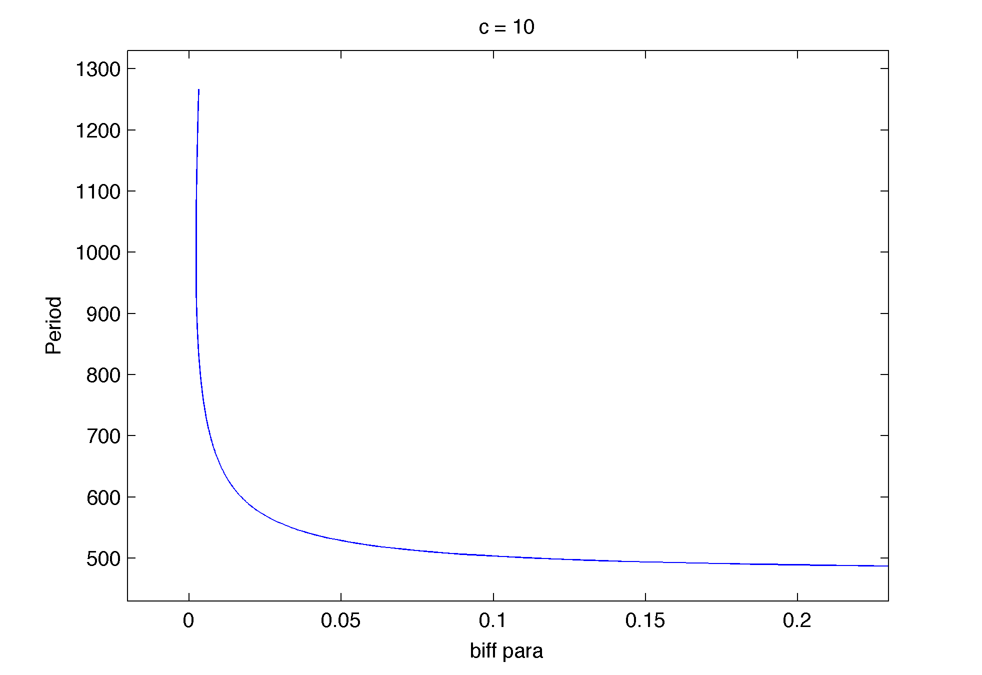
But in this regime the period decrease with the degradation rate, which is not in agreement with the experiment :

Bifurcation diagram in $latex \displaystyle k_{out} $ (there is a fourth Hopf biff around k_out = -10) :

Position the Hopf-bifurcations in the (k_out, c) plane :

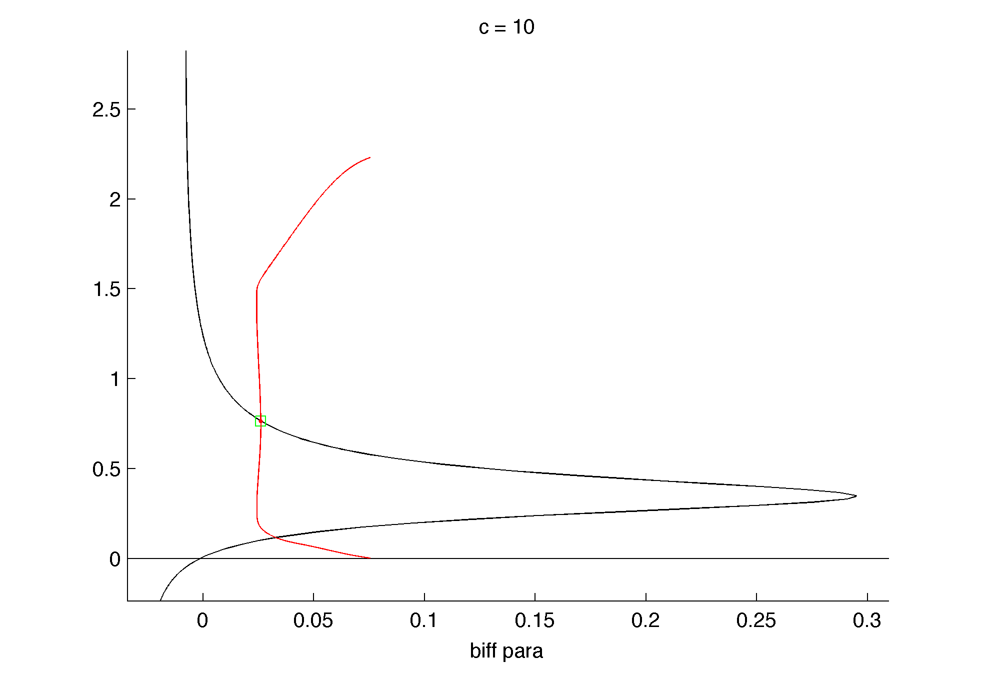
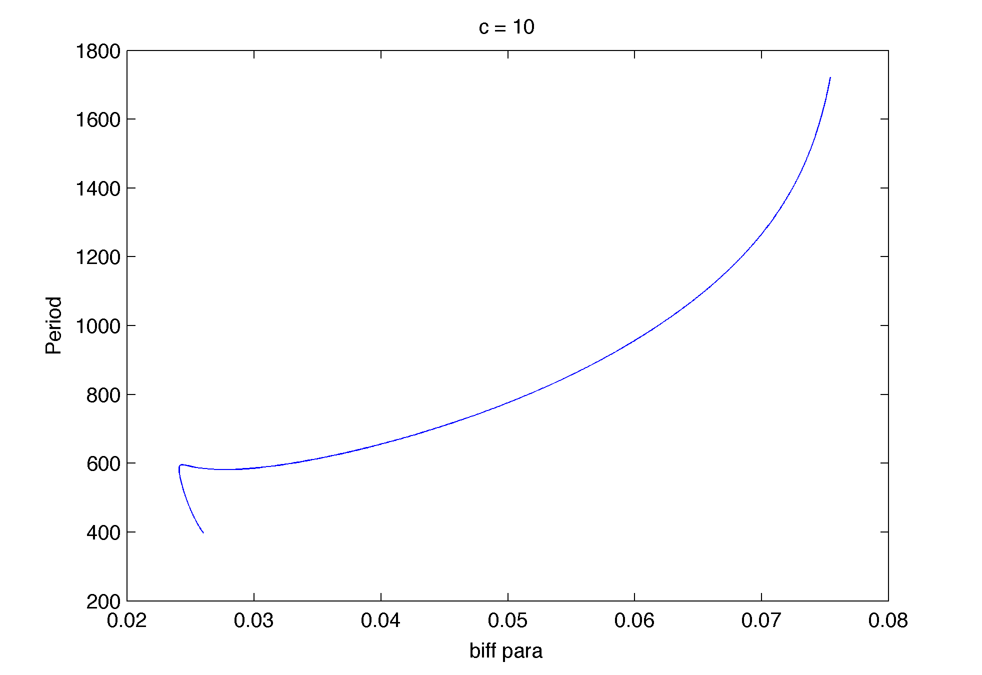
Bifurcation diagram in $latex \lambda_{3} $ again but taking k_out = 0.45 :  

Parameters (in the same order than in the equation) : 10.0000 0.5000 0.0286 0.4500 0.2000 1.0000 0.0286 12 0.5000 0.0400 0.4500 0.0250 1.5000(*1000)

In this regim the period increase with degradation rate, kind of :